
UNED
Research Journal (e-ISSN 1659-441X), Vol. 12(2): e3142, December, 2020
Morfometría de la cuenca alta del río Páez, Costa Rica, y su relación con la infiltración
Pablo Ramírez-Granados1![]() , Allan Astorga-Gättgens2
, Allan Astorga-Gättgens2![]() , Lolita Campos-Bejarano3
, Lolita Campos-Bejarano3![]() & Carlos Henríquez Henríquez4
& Carlos Henríquez Henríquez4![]()
1. Universidad Nacional, Laboratorio de Hidrogeología y Manejo de Recursos Hídricos, Heredia, Heredia, Costa Rica; pablo.ramirez.granados@una.ac.cr
2. Consultor Ambiental, Curridabat, Costa Rica; a.astorga.g@gmail.com
3. Universidad de Costa Rica, Escuela Centroamericana de Geología, San Pedro de Montes de Oca, Costa Rica; l.campos.b@gmail.com
4. Universidad de Costa Rica, Centro de Investigaciones Agronómicas, San Pedro de Montes de Oca, Costa Rica; carlos.henriquez@ucr.ac.cr
Recibido 07-VI-2020 Corregido 09-X-2020 Aceptado 14-X-2020
DOI: https://doi.org/10.22458/urj.v12i2.3142
|
ABSTRACT. “Morphometry of
the upper basin of the Páez River, Costa Rica, and
its relationship with infiltration” Introduction:
Morphometric studies are the basis of the hydrological study of a basin and
have application in soil and water conservation. Little is known about the
upper basin of the Páez River, Costa Rica, whose
springs are used for livestock and vegetable cultivation. Objective: To establish the
morphometry of the basin and evaluate infiltration and potential for
groundwater recharge. Methods: We
used digitized contour lines, every 5m, to build a Digital Elevation Model in
Surfer (triangulation with linear interpolation). Results: The most influencing factor is the variation of the
slopes, which are mostly oriented to the south. Morphometric analysis
generated a rectilinear type curve indicating a state of non-equilibrium.
Most streams are in order 1. The hydrological values of the soils vary
significantly with slope, which, together with the basin shape, cause changes
in groundwater recharge due to infiltration. The quantity of drains of order
1 is related to the permeability of the terrain and infiltration
characteristics. Moderate values of drain density are an indicator of
increased infiltration and of high potential for groundwater recharge. Conclusions: The hydrological
properties of the upper basin of the Páez river are
conditioned by its morphometry, especially by the variations in the slopes
between contours and the dynamics of the drainage network. Keywords: watershed geometry, drainage
network, hypsometric curve, terrain slope, infiltration. |
RESUMEN. Introducción: Los estudios morfométricos
son la base del estudio hidrológico de una cuenca y tienen aplicación en la
conservación de suelos y aguas. Se sabe poco sobre la cuenca alta del río
Páez, Costa Rica, cuyos manantiales son usados en ganadería y cultivo de
vegetales. Objetivo: establecer la morfometría
de la cuenca y evaluar la infiltración el potencial de recarga. Método:
Usamos curvas de nivel digitalizadas, cada 5m, para construir un Modelo de
Elevación Digital en Surfer (triangulación
con interpolación lineal). Resultados: El factor más influyente es la
variación de las laderas, que en su mayoría están orientadas al sur. El
análisis morfométrico generó una forma rectilínea
que indica un estado de “no equilibrio”. La mayoría de los arroyos están en
orden 1. Los valores hidrológicos de los suelos varían significativamente con
la pendiente, lo que, junto con la forma de la cuenca, provoca cambios en la
recarga del agua subterránea debido a la infiltración. La cantidad de
drenajes de orden 1 está relacionada con la permeabilidad del terreno y las
características de infiltración. Los valores moderados de densidad de drenaje
son un indicador de una mayor infiltración y un alto potencial de recarga de
agua subterránea. Conclusiones: Las propiedades hidrológicas de la
cuenca alta del río Páez están condicionadas por su morfometría,
especialmente por las variaciones en las pendientes entre curvas de nivel y
la dinámica de la red de drenaje. Palabras clave: geometría de cuencas, red de drenajes, curva hipsométrica, pendiente del terreno, infiltración.
|
El análisis morfométrico es una medición cuantitativa, basada en el análisis matemático de las características físicas de una cuenca hidrográficas. Los estudios morfométricos constituyen el inicio del análisis de las características hidrológicas de una cuenca (Altin & Altin, 2011) y también tienen aplicación en la conservación de suelos y aguas (Asfaw & Workineh, 2019), la geomorfología tectónica (Bahrami, Capolongo, & Mofrad, 2020) y la composición y diversidad de la vegetación (Al-Rowaily, El-Bana, & Al-Dujain, 2012).
El análisis morfométrico inicialmente fue desarrollado por varios autores, Horton (1932), con las características de la cuenca y el desarrollo de los drenajes, Langbein (1947), con la curva hipsométrica, Schumm (1956), con las características de la red de drenaje, Chorley, Malm, y Pogorzelski (1957), con la estimación de la forma de la cuenca, Strahler (1952), con el análisis de la curva hipsométrica, Gray (1961), con las relaciones entre cuencas, Gregory y Walling (1968), con la relación de la densidad de drenaje dentro de la cuenca.
En morfometría, una forma para estructurar el análisis de cuenca es a partir de los aspectos de esta (Sakthievel, Raj, Sivasankar, Akhila, & Omine, 2019). Se pueden encontrar aspectos lineales (longitud de la cuenca, el orden de las corrientes, la longitud de corrientes, longitud media de corrientes), de área (área de la cuenca, densidad de drenaje, forma de la cuenca, relación de circularidad) y de relieve (relieve de la cuenca, pendiente de la cuenca), estos se pueden calcular para tener una caracterización física apropiada de una cuenca.
Antes del avance de los sistemas de información geográfica y la teledetección, el análisis de las características de una cuenca era una tarea ampliamente operativa y compleja, ahora la mayoría de los aspectos son obtenidos de manera simplificada a partir del modelado en sistemas de información geográfica.
Distintos autores han aplicado morfometría para diferentes aplicaciones entre las cuáles se pueden mencionar, geomorfología (Knight & Grab, 2018; Prabhakaran & Raj; 2018; Bahrami et al., 2020), conservación de aguas y suelos (Asfaw & Workineh, 2019), erosión (Debelo, Tadele, & Koriche, 2017), escorrentía (Abdulkareem, Pradhan, Sulaiman, & Jamil, 2018) y recarga potencial de aguas subterráneas (Zaidi, 2011; Kabite & Gessesse, 2018).
El objetivo del estudio es caracterizar las propiedades morfométricas de la cuenca alta del río Páez en la cual afloran muchos manantiales, los cuales son captados para el aprovechamiento humano, con el fin de relacionar dichas propiedades con los procesos de infiltración.
MATERIALES Y MÉTODOS
Área de estudio: Comprende la parte alta de la cuenca del Río Páez, entre las coordenadas 514 000m y 516 000m este y 1 096 000m y 1 103 000m norte del sistema de proyección Transversal de Mercator para Costa Rica (CRTM). Presenta un área superficial de 6,79km2. Hacia ambos lados de la cuenca, nacen los ríos Reventado y Birrís, los cuales corresponden con sus cuencas vecinas y las cuáles comparten varias similitudes biofísicas. La cuenca alta presenta drenajes de cuarto orden.
Su principal población es San Juan de Chicuá y hacia el sur, al oeste el poblado de Potrero Cerrado. La cuenca alta presenta altitudes máximas arriba de los 3 300m, llegando hasta los 2 200m en la parte baja. El relieve se considera suave, producto de las secuencias de materiales lávicos (Fig. 1).
La zona se caracteriza por ser una cuenca de uso agropecuario, donde se alternan los pastos y los cultivos. Dentro de los cultivos más importantes están la papa, el brócoli, la zanahoria, la coliflor, el repollo, la remolacha y el culantro.
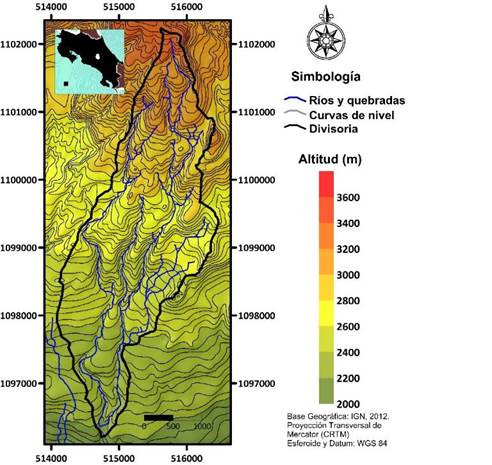
Fig.1. Ubicación de la cuenca alta del río Páez.
Regionalmente, el área de estudio presenta las unidades geológicas Sapper, Birrís y Reventado Miembro Superior (Krushensky, 1972). Localmente, los materiales volcánicos que conforman el área de estudio fueron descritos a partir de algunas perforaciones realizadas en el sector de Prusia, Sanatorio Durán, parque Prusia y la Pastora, todos muy cercanos a la cuenca alta.
Los suelos que conforman la parte alta de la cuenca del río Páez, pertenecen a los órdenes Entisoles y Andisoles. De forma más detallada, en la parte más alta, se reconocen suelos del suborden Orthents y Udands. En la zona de San Juan de Chicuá, dominan los Udands. En la parte sur, los suelos conciernen al suborden Ustands.
En la cuenca, la precipitación alcanza valores promedio anuales mayores a los 1 800mm en el volcán Irazú y aproximadamente 1 500mm en la parte baja de acuerdo con las mediciones del Instituto Meteorológico Nacional (IMN) para el año 2017.
Características morfométricas: La morfometría de la cuenca alta del río Páez, fue obtenida con base en las curvas de nivel digitalizadas, cada 5m, del Gran Área Metropolitana (GAM), escala 1:10 000 del proyecto PRUGAM. Con estas curvas se construyó el Modelo de Elevación Digital (MED) en Surfer, versión 16, usando como método de interpolación la triangulación con interpolación lineal. Del MED se obtuvo el mapa de pendientes en grados y el mapa de orientación del terreno.
Con uso de ArcGis, versión 10,2 y MapInfo, versión 12, se realizó la digitalización de las curvas de nivel, los drenajes y el parteaguas. Una vez obtenidos los elementos principales de la cuenca hidrográfica, se determinó, a partir de los valores de elevación de las curvas de nivel, el MED mediante interpolación lineal o triangulación. Con la herramienta de geometría de ArcGis, se calcularon las siguientes propiedades de la cuenca: área (A), perímetro (P), longitud máxima (Lmax) y ancho máximo (Wmax). Para determinar Lmax se utilizó una circunferencia que envolviera la forma total de la cuenca y para Wmax se obtuvieron polilíneas perpendiculares a los límites de la cuenca para luego calcular la mayor longitud dentro de la cuenca, la definición de ambos siguió los criterios de Zǎvoianu (1985). Como parámetro de corroboración, se calculó la longitud y ancho promedio considerando la forma de la cuenca a ser equivalente a un rectángulo (Roche, 1963; Zǎvoianu, 1985).
Sobreponiendo el vector poligonal de la cuenca a los vectores lineales de los contornos topográficos, cada 5m, se calcularon las áreas parciales entre contornos (Ai) con la herramienta de geometría de ArcGis.
Para el caso de los vectores lineales de ríos y contornos topográficos, se calcularon las longitudes de línea para cada uno. De la forma de la cuenca se computaron los siguientes parámetros: El factor de forma (Ff), definido por Horton (1932) y la relación de circularidad (Rc), definido por Miller (1953).
La curva hipsométrica y el gráfico de frecuencia altimétrica fueron construidos usando las áreas entre contornos determinadas en ArcGis y las elevaciones. El valor de la integral fue obtenido del método de Pike y Wilson (1971).
Mediante ArcGis, se calculó el número de corrientes, la longitud de las corrientes, la textura del drenaje (Horton, 1945), y la frecuencia de drenajes (Horton, 1945). La clasificación de los órdenes de los drenajes fue utilizando el método de Strahler (1957), de ella se obtuvieron la relación de bifurcación (Rb), definida como el cociente del número de corrientes del orden dado (Ni) entre el número de corrientes de orden superior inmediato (Ns), definido por Horton (1945), Schumm (1956) y Zǎvoianu (1985).
Del producto de la densidad de drenaje (Dd) y la densidad de corrientes (Dc), se obtuvo el número de infiltración (Romshoo, Bhat, & Rashid, 2012).
Para establecer la pendiente del cauce principal usando el método de compensación de áreas, se trazó un perfil longitudinal en el MED y este luego fue exportado a una hoja electrónica como un gráfico de dispersión. A este gráfico se le determinó la ecuación de tendencia y la recta de mejor ajuste. Luego se calcularon las áreas parciales arriba y debajo de la línea de tendencia para obtener una nueva ecuación de mejor ajuste.
RESULTADOS
Geometría: La cuenca alta del río Páez tiene un área, A = 6,80km2, con un perímetro, P = 15km y se encuentra delimitada entre los contornos altitudinales de 2 160 a 3 315m (Fig. 2). En el MED las elevaciones de la cuenca disminuyen desde el norte hacia el sur de forma gradual.
El área promedio entre los contornos topográficos es de 0,03km2, por cada 5m de elevación del terreno, la desviación respecto a la media para el área entre contornos muestra valores de 0,15 km2. La separación media entre los contornos topográficos cada 5m, obtenida por el rectángulo equivalente, es de 28,01m. Al usar la relación entre la altitud de contornos y la separación entre ellos, se obtiene el valor de la pendiente media entre contornos calculada en 15,72° con máximas de 89,01° y mínimas de 4,64°, esto también puede ser observado en el modelo de pendientes (Fig. 3), donde se puede apreciar que la mayoría de las pendientes dominantes en la cuenca alta son las que van del rango de 0 a 20° con valores altos de 30 a 40 grados en los cañones de los ríos y valores máximos de más de 50°.
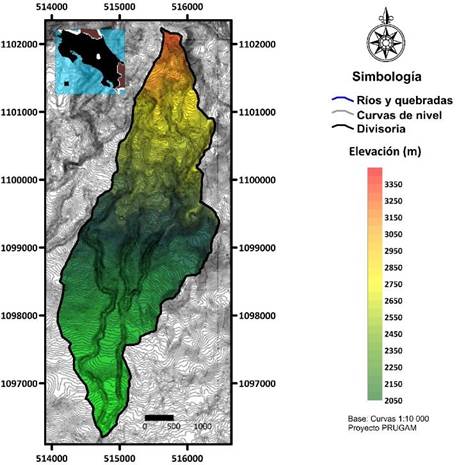
Fig. 2. Modelo de Elevación Digital (MED) de la cuenca alta del río Páez.
El área promedio entre los contornos topográficos es de 0,03km2, por cada 5m de elevación del terreno, la desviación respecto a la media para el área entre contornos muestra valores de 0,15 km2. La separación media entre los contornos topográficos cada 5m, obtenida por el rectángulo equivalente, es de 28,01m. Al usar la relación entre la altitud de contornos y la separación entre ellos, se obtiene el valor de la pendiente media entre contornos calculada en 15,72° con máximas de 89,01° y mínimas de 4,64°, esto también puede ser observado en el modelo de pendientes (Fig. 3), donde se puede apreciar que la mayoría de las pendientes dominantes en la cuenca alta son las que van del rango de 0 a 20° con valores altos de 30 a 40 grados en los cañones de los ríos y valores máximos de más de 50°.
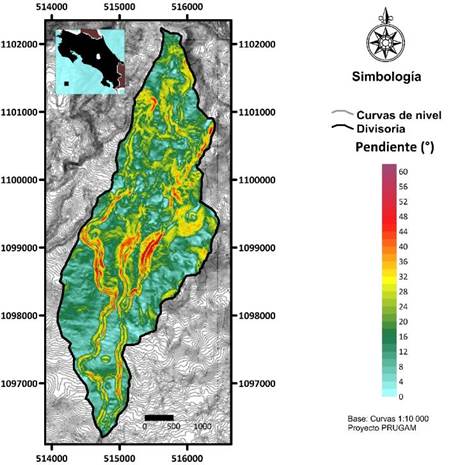
Fig. 3. Pendientes de la cuenca alta del río Páez.
Al considerar las pendientes con respecto a los contornos de elevación, se puede visualizar con mayor detenimiento que las pendientes aumentan en la cuenca baja y en la cuenca alta, con variaciones significativas de la tendencia, la cual en general está debajo de los 10° entre los 2 360 y los 2 800m (Fig. 4).
En lo respecta a la orientación, se obtuvo el mapa de aspecto (Fig. 5) basado en la dirección de la pendiente. En la cuenca alta del río Páez, las pendientes están orientadas predominantemente hacia el sur, y en menor media hacia el suroeste y este.
El largo y ancho de la cuenca, calculados con el criterio del rectángulo equivalente, obtuvo valores de 6,44 y 1,05km respectivamente, los cuáles son muy próximos a los valores reales de la cuenca alta calculados por geometría de vectores en ArcGis, 6,08 y 1,11km respectivamente. El valor del índice pendiente calculado con el lado mayor, L, fue de 0,40. El valor del factor de forma fue de 0,18.
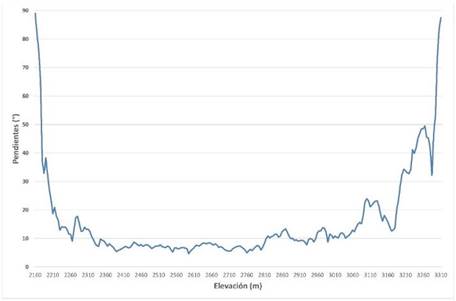
Fig. 4. Relación entre las pendientes de la cuenca según rango de elevación.
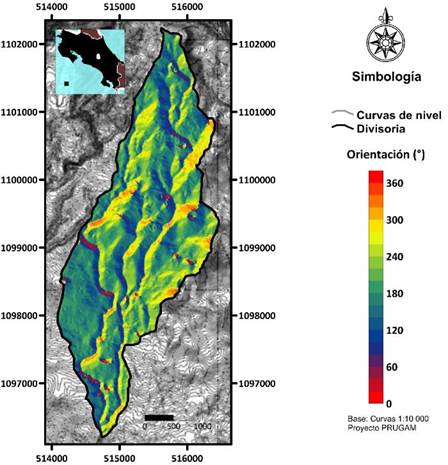
Fig. 5. Aspecto de la cuenca alta del río Páez.
Análisis hipsométrico: La cuenca alta del río Páez muestra una curva hipsométrica del tipo rectilíneo (Fig. 6), con pequeños puntos de inflexión apenas notables en la parte alta y baja de la curva. Esta forma rectilínea está asociada directamente al hecho de que esta cuenca corresponde con la parte alta de la cuenca del río Páez. El valor de la integral hipsométrica fue calculado en 0,5.
La curva de frecuencia de altitudes (Fig. 7) mostró como la mayoría del área de la cuenca alta se concentra entre los contornos altimétricos entre los 2 360m y los 3 060m.
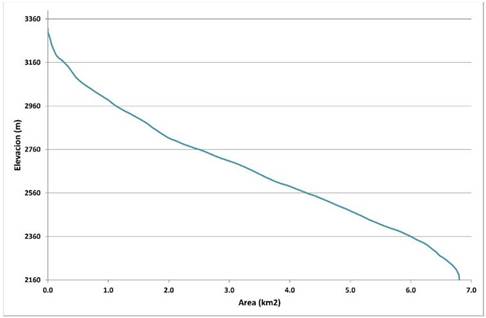
Fig. 6. Curva hipsométrica de la cuenca alta del río Páez.
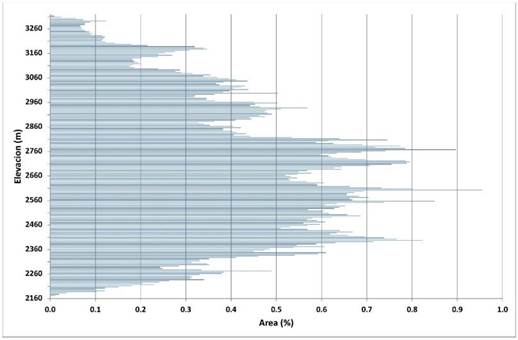
Fig. 7. Frecuencia altimétrica de la cuenca alta del río Páez.
Red de drenaje: La cuenca alta del río Páez tiene un orden de drenaje de 5, de acuerdo con el método de Strahler. Las longitudes de las corrientes disminuyen de acuerdo con el orden (Cuadro 1) Por orden, las corrientes de orden 1 corresponden con un 43,55% del total de la longitud de los drenajes, mientras que el orden 4 le sigue con un 22,13% y muy cerca los órdenes de 2 y de 3 con un 17,37 y 16,59% (Fig. 8). En total las corrientes de orden 1 constituyen un 70,98% del total de corrientes clasificadas.
CUADRO 1
Relación de la longitud y el número de corrientes
|
Orden |
Longitud (Km) |
Número de corrientes |
|
1 |
19,58 |
137 |
|
2 |
7,81 |
33 |
|
3 |
7,46 |
19 |
|
4 |
9,95 |
3 |
|
5 |
0,16 |
1 |
|
Total |
44,97 |
193 |
La relación entre el orden de las corrientes y la longitud de ellas responde a una función exponencial.
En cuanto a la pendiente media del cauce de la cuenca alta del río Páez, esta fue estimada con el criterio de la compensación de áreas.
La ecuación que modela la pendiente del cauce principal en la cuenca alta del río Páez fue:
![]()
donde H = es la altitud (m) y L = la longitud de la trayectoria del drenaje (m). En este caso, la pendiente del cauce principal fue estimada en 0,1617.
La relación de bifurcación entre los órdenes fue la siguiente: 4,15 para los órdenes 1 y 2, 1,74 para los órdenes 2 y 3, 6,33 para los órdenes 3 y 4; y 3,00 para los órdenes 4 y 5.
En cuanto a la densidad de corrientes, el valor obtenido fue de 28,36/km2, mientras el valor de la densidad de drenajes es 6,60 km/km2.
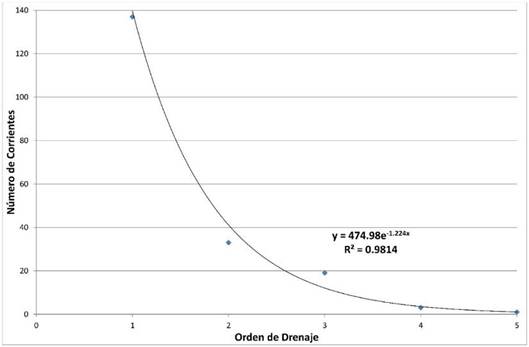
Fig.8. Relación del orden de los drenajes y su número correspondiente.
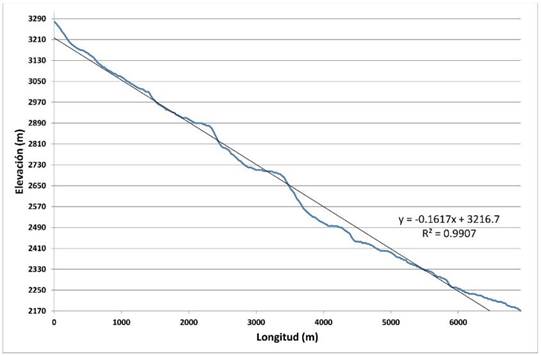
Fig. 9. Perfil longitudinal del cauce principal y pendiente media obtenida por el criterio de la compensación de área.
DISCUSIÓN
Geometría: En el área entre contornos, los valores altimétricos cambian en una distancia promedio entre contornos de 28,01m, esto implica distintos valores de pendiente que pueden condicionar la infiltración en distintos puntos de la cuenca, lo cual es respaldado por otros autores (Domínguez & Mercado, 2020) que consideran que la pendiente es uno de los principales factores que influyen en la infiltración de la lluvia. En cuanto a los rangos de pendientes y su relación con la infiltración, Ribolzi et al. (2011), indican que los rangos de 75% (36,87°) reciben menos agua por infiltración que las de 30% (16,7°). Morbidelli et al. (2016) indican que en los ensayos realizados con pendientes entre los 10 a 15°, hay una disminución en el valor de conductividad hidráulica saturada. Considerando la clasificación de pendientes de Singh, Gupta, y Singh (2014), la mayoría de la cuenca presenta valores de pendiente entre 10 a 35° estas favorecen la escorrentía y disminuyen la infiltración (Singh et al., 2014). En cuanto al aspecto del terreno, este influye en las características de los suelos, causando que en las zonas de menor insolación puedan existir mayores contenidos de humedad (Geroy et al., 2011).
Con respecto a los parámetros geométricos, la estimación de la longitud y el ancho de la cuenca mediante el rectángulo equivalente es una buena aproximación como herramienta sustitutiva de la medición de los valores reales de longitud y ancho de la cuenca. La aplicación de este método difiere en 360m en la longitud y 62m en el ancho por lo que puede ser usado como un método alternativo en geometrías complejas de las cuencas. Para el factor de forma, el valor obtenido fue de 0,1838, este valor es concordante con otros valores de factor de forma encontrados en otras cuencas (Kumar, Mohan, Mishra, Ahmad, & Mishra, 2014; Sakthievel et al., 2019). Para la cuenca alta del río Páez, el valor del factor de forma señala que esta es una cuenca de tipo elongada donde los movimientos de crecidas son más fáciles de controlar que en cuencas circulares (Debelo et al., 2017). Debido a su factor de forma y a su consecuente forma alargada, algunos autores mencionan que se propicia la recarga de aguas subterráneas (Soni, 2016, Abdulkareem et al., 2018) debido a que tendrán un pico de flujo de moderado a bajo (Singh et al., 2014), caracterizado por hidrogramas planos (Fenta, Yasuda, Shimizu, Haregeweyn, & Woldearegay, 2017).
Análisis hipsométrico: La curva hipsométrica que presenta la cuenca es de tipo rectilínea y expresa la forma de la cuenca de drenaje y la evolución de su paisaje (Asfaw & Workineh, 2019). Debido a su forma, esta refleja un estado de no equilibrio (Strahler, 1952). El valor de la integral hipsométrica fue calculado en 0,5 lo que indica que es una cuenca tectónicamente estable (Kumar & Joshi, 2015) y la cual está en equilibrio o casi en madurez (Asfaw & Workineh, 2019).
Red de drenaje: El análisis de la red de drenaje es uno de los parámetros morfométricos que mejor pueden describir el comportamiento hidrogeológico de una cuenca, entre los cuáles se destacan la infiltración (Kumar & Joshi, 2015) y el comportamiento del flujo de agua vertical y horizontal en la superficie del terreno (Singh et al., 2014).
El incremento en el número de orden, de 1 a 5 (Cuadro 1), se relacionada directamente con el tamaño de la cuenca (Kumar & Joshi, 2015) como también con la continua erosión de las orillas de los ríos, esto último observable en distintos sectores de la cuenca. La relación del número del número de corrientes con respecto a su orden permite establecer una ecuación a partir de una función exponencial, esta función puede ser utilizada para comparar cuencas semejantes (Kabite & Gessesse, 2018). La cuenca presenta un patrón dendrítico el cual es un indicador de la homogeneidad del estrato subsuperficial (Singh, et al., 2014) en este caso materiales volcánicos como cenizas, tobas y lavas.
El total del número de corrientes de la cuenca brinda información sobre los factores de escorrentía superficial (Rai, Chandel, Mishra, & Singh, 2018) y por lo tanto de su relación con la infiltración. Para la cuenca el valor máximo de corrientes de orden 1 es de 137 corrientes lo cual designa la intensidad de la permeabilidad y las características de infiltración del área (Kumar & Joshi 2015; Rai et al., 2018).
Un perfil longitudinal de una corriente es una propiedad de la geometría de las corrientes que puede dar pistas sobre los materiales subyacentes (Hack,1973). Con respecto a la pendiente media del cauce principal, determinada del perfil longitudinal, con el criterio de la compensación de área, este incide directamente en la velocidad de un caudal a lo largo del cauce y condiciona su energía cinética y por lo tato su capacidad erosiva (Campo, Aldalur, & Fernández, 2012). En la figura 9, a lo largo del perfil longitudinal del cauce principal, en su recorrido son observables sectores de fuerte pendiente que están relacionados a saltos o cataratas, los cuales son asociados a frentes de coladas volcánicas y a la aparición de manantiales.
La relación de bifurcación definida por Horton (1945) es un índice de relieve y disecciones (Kumar & Joshi, 2015). Strahler (1957) indica que los valores entre 2 a 5 en cuencas con una red de drenaje bien desarrollada y presentan unidades geológicas relativamente homogéneas (Liaqat, Rehman, & Alia, 2011). En el caso de valores de 2, estos corresponden con una región plana (Horton, 1945) y de 3 a 4 para terreno montañoso y altamente disectado. Para la cuenca alta del río Páez, los valores obtenidos para la relación de bifurcación muestran que algunas de las zonas donde ocurren la relación de bifurcación para los órdenes 2 y 3 corresponden con zonas planas, mientras que las de los órdenes 1 y 2, 3 y 4; y 4 y 4 están relacionadas a zonas de crecidas repentinas durante una tormenta fuerte (Kumar & Joshi, 2015). Estas diferencias en los valores de la relación de bifurcación indican diferencias en el estado geomorfológico y las diferencias topográficas en la cuenca (Bhatt & Ahmed, 2014).
El valor de la densidad de drenajes de la cuenca es de 6,6km/km2, esto le da un valor de textura de drenaje de fino, este valor de la textura de drenaje depende de varios factores como lo son el clima, la lluvia, la vegetación, la roca, el tipo de suelo, la capacidad de infiltración y el relieve de la cuenca (Singh et al., 2014). Los valores altos de densidad de drenaje son el resultado de material subsuperficial débil o impermeable, vegetación ligera y relieve montañoso. Los valores bajos de la densidad de drenaje de una cuenca revelan que ellos están compuestos de material subsuperficial permeable, buena cubierta de vegetación y bajo relieve, lo cual resulta en una mayor capacidad de infiltración de en la cuenca (Singh et al., 2014). El valor de fino de la cuenca alta del río Páez es un valor medio, pues combina poca vegetación, al ser una cuenca con fines agrícolas donde el terreno pasa muy descubierto y materiales permeables. Kumar y Joshi (2015) indican que los valores de densidad de drenajes moderado corresponden con mayor infiltración de agua y un alto potencial de recarga de aguas subterráneas, en el caso de la cuenca, el valor es ligeramente más bajo.
AGRADECIMIENTOS
Los autores expresan su agradecimiento al Laboratorio de Hidrogeología y Manejo de Recursos Hídricos de la Universidad Nacional por el apoyo brindado en la investigación.
ÉTICA, CONFLICTO DE INTERESES Y DECLARACIÓN DE FINANCIAMIENTO
Los autores haber cumplido con todos los requisitos éticos y legales pertinentes, tanto durante el estudio como en el manuscrito; que no hay conflictos de interés de ningún tipo, y que todas las fuentes financieras se detallan plena y claramente en la sección de agradecimientos. Asimismo, están de acuerdo con la versión editada final del documento. El respectivo documento legal firmado se encuentra en los archivos de la revista.
La contribución de los autores es como se detalla a continuación: P.R.G.: escritura del artículo, elaboración de los mapas,análisis morfométrico, revisión de las referencias. A.A.G., L.C.B. y C.H.H.: revisión del manuscrito”
REFERENCIAS
Abdulkareem, J., Pradhan, B., Sulaiman, W., & Jamil, N. (2018). Quantification of
runoff as influenced by morphometric characteristics in a rural complex
catchment. Earth Systems and Environment, 2, 145-162. DOI:
10.1007/s41748-018-0043-0
Al-Rowaily, S., El-Bana,
M., & Al-Dujain, F. (2012). Changes in vegetation
composition and diversity in relation to morphometry, soil and grazing on a
hyper-arid watershed in the central Saudi Arabia. Catena, 97, 41-49.
DOI: 10.1016/j.catena.2012.05.004
Altin, T., & Altin, B.
(2011). Development and morphometry of drainage network in volcanic terrain,
Central Anatolia, Turkey. Geomorphology, 125: 485-503. DOI:
10.1016/j.geomorph.2010.09.023
Asfaw, D., & Workineh,
G. (2019). Quantitative analysis of morphometry on Ribb
and Gumara watersheds: Implications for soil and
water conservation. International Soil and Water Conservation Research, 7(2),
150-157. DOI: 10.1016/j.iswcr.2019.02.003
Bahrami, S., Capolongo,
D., & Mofrad, M. (2020). Morphometry of drainage
basins and stream network as an indicator of active fold growth (Gorm anticline, Fars Province, Iran). Geomorphology,
355, 1-20. DOI: 10.1016/j.geomorph.2020.107086
Bhatt, S., & Ahmed, S. (2014). Morphometric analysis to determine floods in the Upper Krishna basin using Cartosat DEM. Geocarto International, 29(8), 878-894. DOI: 10.1080/10106049.2013.868042
Campo, A., Aldalur, N., & Fernández, S. (2012). Morfometría fluvial aplicada a una cuenca urbana en
Ingeniero White, República Argentina. Investigaciones Geográficas, (77), 7-17.
Chorley, R., Malm, D., & Pogorzelski, H. (1957). A new standard for estimating drainage
basin shape. American Journal of Science, 255, 138-141.
Debelo, G., Tadele, K.,
& Koriche, S. (2017). Morphometric analysis to
identify erosion prone areas on the Upper Blue Nile using GIS (Case study of Didessa and Jema sub-basin,
Ethiopia). International Research Journal of Engineering and Technology,
4(8), 1773-1784.
Domínguez, F., & Mercado, T. 2020. Potential inifiltration and morphometry in Arroyo Grande basin, Sucre, Colombia. Revista Facultad de Ingeniería Universidad de Antioquia, 96, 21-31.
Fenta, A., Yasuda, H., Shimizu, K., Haregeweyn, N.,
& Woldearegay, K. (2017). Quantitative
analysis and implications of drainage morphometry of the Agula
watershed in the semi-arid northern Ethiopia. Applied Water Science, 7,
3825-3840.DOI: 10.1007/s13201-017-0534-4
Geroy, I., Gribb, M.,
Marshall, H., Chandler., D; Benner, S., & McNamara, J. (2011). Aspect
influences on soil water retention and storage. Hydrological Processes, 25(25),
3836-3842. DOI: 10.1002/hyp.8281
Gray, D. (1961). Interrelationships of watershed characteristics. Journal
of Geophysical Research, 66 (4), 1215-1223.
Gregory, K., & Walling, D. (1968). The variation of drainage density
within a catchment. International Association of Scientific Hydrology
Bulletin, 13(2), 61-68.
Hack, J. (1973). Stream-profile and stream-gradient index. Journal of
Research United States Geological Survey, 1(4), 421-429.
Horton, R. (1932). Drainage-basins characteristics. Transactions
American Geophysical Union, 13(1), 350-361.
Horton, R. (1945). Erosional development of streams and their drainage
basins; hydrophysical approach to quantitative
morphology. Geological Society of America Bulletin, 56, 275-370.
Kabite, G., & Gessesse,
B. (2018). Hydro-geomorphological characterization of Dhidhessa
river basin, Ethiopia. International Soil and Water Conservation Research,
6(2), 175-183. DOI: 10.1016/j.iswcr.2018.02.003
Knight, J., & Grab, S. (2018). Drainage network morphometry and
evolution in the eastern Lesotho highlands, southern Africa. Quaternary
International, 470 (part A), 4-17. DOI: 10.1016/j.quaint.2017.07.024
Krushensky, R. (1972). Geology of Istaru Quadrangle, Costa Rica. Washington: United
States Geological Survey. DOI: 10.3133/b1358
Kumar, P., Mohan, K., Mishra, S., Ahmad, A., & Mishra, V. (2014). A
GIS-based approach in drainage morphometric analysis of Kanhar
river basin, India. Applied Water Science, 7:16.
Kumar, P., & Joshi, V. (2015). Characterization of hydro geological
behavior of the upper watershed of river Subarnarekha through morphometric
analysis using remote sensing and GIS approach. International Journal of
Environmental Sciences, 6(4), 429-447. DOI: 10.6088/ijes.6049
Langbein, W. (1947). Topographic
characteristic of drainage basins. Water-Supply Paper United States
Geological Survey 968-C: 125-157.
Liaqat, R., Rehman, A.,
& Alia, Y. (2011). Morphometric analysis of drainage basin using remote
sensing and GIS techniques: A case study of Etmadpur
Tehsil, Agra district, U.P. International Journal of Research in Chemistry
and Environment, 1(2), 36-45.
Miller, V. (1953). A quantitative geomorphic study of drainage basin
characteristics in the Clinch mountain area. New York: Columbia University.
Morbidelli, R., Saltalippi,
C., Flammini, A., Cifrodelli,
M., Picciafouco, T., Corradini,
C., & Govindaraju, R. (2016). Laboratory
investigation on the role of slope on infiltration over grassy soils. Journal
of Hydrology, 543 (part B), 542-547. DOI: 10.1016/j.jhydrol.2016.10.024
Pike, R., & Wilson, S.
(1971). Elevation-relief ratio, hypsometric integral, and geomorphic
area-altitude analysis. Geological Society of America Bulletin, 82(4),
1079-1084. DOI: 10.1130/0016-7606(1971)82[1079:ERHIAG]2.0.CO;2
Prabhakaran, A., & Raj, N. (2018).
Drainage morphometric analysis for assessing form and processes of the
watersheds of Pachamalai hills and its adjoinings, Central Tamil Nadu, India. Applied Water
Science, 8(1),31. DOI: 10.1007/s13201-018-0646-5
Rai, P., Chandel, R., Mishra, V., & Singh,
P. (2018). Hydrological inferences through morphometric analysis of lower Kosi river basin of India for water resource management
based on remote sensing data. Applied Water Science, 8, 15. DOI:
10.1007/s13201-018-0660-7.
Ribolzi, O., Patin,
J., Brenson, L., Latsachack,
K., Mouche, E., Sengtaheuanghoung,
O., Silvera, N., Thiébaux,
J., & Valentin, C. (2011). Impact of slope gradient on soil surface
features and infiltration on steep slopes in northern Laos. Geomorphology
127(1-2), 127: 53-63. DOI: 10.1016/j.geomorph.2010.12.004.
Roche, M. (1963). Hydrologie de
Surface. París: Guathier-Villars
Editeur.
Romshoo, S., Bhat, S., & Rashid,
I. (2012). Geoinformatics for assessing the
morphometric control on hydrological response at watershed scale in the Upper
Indus basin. Journal of Earth System Science, 121, 659-686. DOI: 10.1007/s12040-012-0192-8
Sakthievel, R., Raj, N., Sivasankar, V., Akhila, P., &
Omine, K. (2019). Geo-spatial technique-based approach
on drainage morphometric analysis at Kalrayan Hills,
Tamil Nadu, India. Applied Water Science, 9(1), 24. DOI:
10.1007/s13201-019-0899-7
Schumm, S. (1956). Evolution of drainage systems and
slopes in Badlands at Perth Amboy, New Jersey. Bulletin of the Geological
Society of America, 67(5): 597-646. DOI: 10.1130/00167606(1956)67[597:EODSAS]2.0.CO;2
Singh, P., Gupta, A., & Singh, M. (2014). Hydrological inferences
from watershed analysis for water resources management using remote sensing and
GIS techniques. The Egyptian Journal of Remote Sensing and Space Sciences,
17(5), 111-121. DOI: 10.1016/j.ejrs.2014.09.003
Soni, S. (2016). Assessment of morphometric
characteristics of Chakrar watershed in Madhya
Pradesh India using geospatial technique. Applied Water Science, 7,
2089-2102. DOI: 10.1007/s13201-016-0395-2
Strahler, A. (1952). Hypsometric
(area-altitude) analysis of erosional topography. Bulletin of the Geological
Society of America, 53(11), 1117-1142. DOI: 10.1130/00167606(1952)63 [1117:
HAAOET] 2.0.CO;2
Strahler, A. (1957). Quantitative
analysis of watershed geomorphology. Transaction American Geophysical Union,
38(6), 913-920. DOI: 10.1029/TR038i006p00913
Zaidi, F. (2011). Drainage basin morphometry for identifying zones for
artificial recharge: A case study from the Gagas
River Basin, India. Journal Geological Society of India, 77, 160-166. DOI: 10.1007/s12594-011-0019-2
Zăvoianu, I. (1985). Morphometry of Drainage Basins. Amsterdam: Elsevier.