La unidad experimental (parcela) es el área en la que se lleva a cabo la asignación aleatoria de los tratamientos en una prueba crítica (Gomez, 1972). Barros y Tavares (1995) la definen como la unidad básica que provee la información en la cual se basa la experimentación.
Esta información, que se convertirá en los resultados del ensayo, proviene de pruebas de naturaleza probabilística y, por lo tanto, está ligada no solo al comportamiento que puede expresar un determinado tratamiento sino que a otros factores ajenos al mismo, que tienden a opacar su verdadero efecto, llamados en conjunto: error experimental (Barrientos, 1981).
Idealmente las unidades experimentales deberían ser homogéneas, de modo que luego de aplicarles distintos tratamientos se pueda decir que la diferencia (si la existe) es exclusivamente producto del efecto de los tratamientos aplicados y no debido a otros factores ruido. Sin embargo, conseguir una unidad experimental totalmente homogénea cuando se realiza ensayos en el campo es imposible pues siempre prevalecerá la variabilidad intrínseca del material con que se trabaje, el efecto del medio, la variabilidad del suelo, la dinámica de muchas otras poblaciones que pueblan la microflora y microfauna del sitio donde se realice el ensayo, etc. Por lo tanto, si se desea que los resultados de un ensayo sean confiables se debe aplicar técnicas experimentales adecuadas, entre las que se recomienda utilizar un tamaño y una forma adecuados de unidad experimental (Párraga & Chacín, 2000a).
La bibliografía especializada señala dos razones de primordial importancia para justificar la necesidad de estimar un tamaño y una forma óptimos de unidad experimental (Rodríguez et al.1993; Sánchez et al. 2006). La primera es reducir el error experimental del ensayo; la segunda se basa en aspectos económicos y prácticos, como ahorro de semilla, espacio, recursos económicos y trabajo.
Parcelas con un tamaño inferior al óptimo pueden dar resultados poco confiables, por otro lado parcelas grandes pueden incurrir en gastos innecesarios de tiempo y recursos (Gomez, 1972). Así pues, la mayor eficiencia de un ensayo se fundamenta en un tamaño y una forma óptimos de unidad experimental (Vallejo y Mendoza, 1992).
Para determinar el tamaño y la forma de parcela existen métodos estadísticos muy variados, la mayoría parten de un ensayo blanco o ensayo de uniformidad (Rodríguez et al.,1993; Custódio, 2010; Santos et al. 2012). Si bien existen otros métodos, este es el más preciso, con el inconveniente de que requiere de una inversión considerable de tiempo y recursos (Alvarez et al.,1986).
El ensayo blanco es una parcela de extensión relativamente grande que es tratada en toda su superficie uniformemente en cuanto a fertilización, aplicación de agroquímicos y demás labores de cultivo y que a la hora de la cosecha se subdivide en parcelas pequeñas (unidades básicas). Posterior a esto, las unidades básicas se agrupan de manera que formen parcelas de diferentes formas y tamaños, a estas parcelas resultantes se les cuantifica el rendimiento correspondiente mediante la adición de los rendimientos de las unidades básicas. La comparación de cada tipo de parcela se hace por contraste del error probable, error típico o al coeficiente de variación habido en el grupo de parcelas de un tipo y de otro tipo (Rosselló & Fernández, 1986; Kavitha, 2010).
El método de curvatura máxima asocia en un gráfico de dispersión la variable independiente que sería el tamaño de parcela - producto de la combinación de unidades básicas - contra la variable dependiente que sería el coeficiente de variación calculado para cada tamaño. En la gráfica resultante se localiza el punto de curvatura máxima por inspección visual y ese punto corresponde al tamaño óptimo de unidad experimental (Escobar, 1981). No obstante, ese punto también se puede definir cuando al incrementar una unidad en el tamaño de parcela, el coeficiente de variación presenta una reducción del 1%; esto es, cuando la primera derivada de la función que modela la relación entre el coeficiente de variación y el tamaño de parcela es igual a menos uno (Barrientos, 1981; Escobar et al.,1990).
Para determinar la forma se consideran las variancias de todas las posibles formas de un mismo tamaño de unidad experimental y por medio de la prueba de Levene se selecciona la que tenga una variancia significativamente menor (Calero, 1965; Mamani, 1971)
Los ensayos de uniformidad también permiten el estudio de la heterogeneidad del suelo (Gomez & Gomez, 1984), factor que está muy ligado a la definición del tamaño adecuado de unidad experimental. Esta variabilidad de los suelos puede deberse a factores físicos, químicos o biológicos y que, junto con otros factores como la genética del cultivo y las características del sitio, introducen variación en variables como la producción de un cultivo y que se conoce como error experimental (Box et al., 2008).
La uniformidad del suelo puede ser estimada por medio del índice de Smith (1938); este índice relaciona por medio de una regresión los tamaños de parcela, obtenidos por agrupación de unidades básicas provenientes de un ensayo blanco y la variancia unitaria asociada a cada tamaño. El valor absoluto de la pendiente obtenida en la regresión se emplea como índice de homogeneidad del suelo; si es cercano a cero se considera que el suelo es homogéneo y si es cercano a uno heterogéneo.
El objetivo general de este trabajo fue determinar un tamaño y una forma adecuados de parcela para ensayos de rendimiento con maíz en la zona de Santa Cruz, Guanacaste, mediante el método de curvatura máxima; asimismo, calcular el índice de heterogeneidad de Smith y generar un mapa de heterogeneidad del suelo utilizando la variable producción.
MATERIALES Y MÉTODOS
Generalidades: El ensayo se llevó a cabo durante los meses de junio a septiembre del año 2015, en la Finca Experimental de Santa Cruz, propiedad de la Universidad de Costa Rica, situada en el cantón de Santa Cruz, distrito de Santa Cruz, provincia de Guanacaste. La misma se encuentra a 54msnm; posee una precipitación promedio de 1 834mm/año, temperatura media anual de 27,9ºC, con evaporación media diaria de 6,8mm y radiación solar global diaria de 18,7MJ (Instituto Meteorológico Nacional, 2011).
Se empleó la técnica del ensayo blanco descrita por Rodríguez et al. (1993). De acuerdo con este método se sembró una parcela de maíz de 26m X 26m, es decir, de 676m2. De la cual se dejó tres metros de borde alrededor de todo su perímetro; así se obtuvo un área de 20m X 20m (400m2) para ejecutar el ensayo blanco.
La parcela seleccionada tuvo su propia entrada y salida de agua; esto para que no fuera afectada por el agua procedente de otras áreas que pudiera acarrear fertilizantes u otros agroquímicos que intervinieran con el tratamiento uniforme que la misma recibió; además, esta parcela se seleccionó pues representaba las condiciones de la mayoría de la finca en cuanto a topografía y tipo de suelo.
Para la siembra se utilizó semilla de maíz del híbrido HS5G.Esta se llevó a cabo de forma manual, en surcos separados a 1 metro y con una distancia entre plantas de 0,25m para una densidad de 40 000 plantas*ha-1. El manejo que recibió la parcela fue el mismo en todo lo relativo a fertilización, combate de arvenses, plagas y enfermedades.
Labores de campo: Cincuenta días después de la siembra se diseñó una cuadrícula sobre la parcela; para esto se empleó estacas de bambú y cuerdas, de modo que se identificarán claramente las 400 subparcelas (unidades básicas). Cada unidad básica correspondió a una hilera de un metro lineal. Además, cada una recibió coordenadas cartesianas que la ubicaran y la identificaran en el terreno; ambas coordenadas estuvieron dadas por distancias en metros a ejes cartesianos (X será el ancho y Y el largo de la parcela) que coincidieron con los bordes de la parcela.
Se cosechó el elote entero de cada planta perteneciente a cada unidad básica y se colocaron en un saco previamente identificado con el número correspondiente según el sistema de coordenadas cartesianas. Se pesó cada uno de los sacos y se obtuvo la producción en gramos.
Análisis de datos: Se programó una hoja electrónica utilizando el programa Office Excel (Microsoft Corporation©), donde se ingresaron todos los datos correspondientes a la producción de cada unidad básica y se calculó: la variancia y el coeficiente de variación (C.V.) para cada una de las posibles formas y tamaños de unidades experimentales (llamadas también: unidades secundarias) que se obtuvieron por medio de la combinación de las unidades básicas. Se partió de una sola unidad básica hasta llegar a una parcela del tamaño de todas las unidades básicas unidas.
Posteriormente, en un sistema cartesiano, los distintos tamaños de parcela se colocaron en el eje X, mientras que Y fue el eje para los coeficientes de variación; el conjunto de puntos XY generó una dispersión a la que se le ajustó una curva que relaciona tamaño de parcela con variación (Mamani, 1971).
Cabe mencionar que se utilizaron únicamente las combinaciones que resultaban en tamaños de parcela que se ajustaran exactamente al área total de 400 m2, es decir, que la multiplicación del número posible de unidades secundarias por su respectivo tamaño debe ser igual al área total, ya que la metodología así lo establece (Gomez & Gomez, 1984).
Para poder cuantificar la heterogeneidad del suelo, se utilizó el método que Smith (1938) propuso; este se basa en la relación empírica entre el tamaño de unidad experimental y la variancia para la variable rendimiento (g) asociada a cada tamaño, expresada por la siguiente ecuación:
log Vx = log V1 – b log X Ec. 1
Donde
Vx = variancia del rendimiento entre unidades secundarias de “x” unidades.
V1 = variancia del rendimiento entre parcelas unitarias.
X = área de las parcelas secundarias en los diferentes arreglos.
b = coeficiente de heterogeneidad del suelo.
El coeficiente b mide el grado de relación entre el tamaño de unidades experimentales y sus variancias (Mamani, 1971); este coeficiente es conocido como índice de heterogeneidad del suelo o índice de Smith (Centro Internacional de Agricultura Tropical, 1982) y cuyo valor brinda una medida cuantitativa de cuan variable es el suelo en un área determinada (Gomez & Gomez, 1984).
RESULTADOS
Coeficiente de variación: Los coeficientes de variación provenientes de la variable producción en gramos que corresponde a cada tamaño de unidad experimental, conformado por la agrupación de unidades básicas, se presentan en el cuadro 1. En este se observa que el mayor coeficiente de variación fue el correspondiente a un tamaño de unidad experimental de 1 unidad básica que es el menor tamaño posible, mientras que el menor coeficiente de variación estuvo asociado a un tamaño de 200 unidades básicas, que es el mayor tamaño que se puede obtener capaz de generar una medida de variabilidad para este ensayo de uniformidad. Se nota que conforme aumenta el tamaño de unidad experimental disminuye el promedio del coeficiente de variación, sin embargo, esta disminución del coeficiente de variación se hace cada vez más pequeña conforme aumenta el tamaño de la unidad experimental.
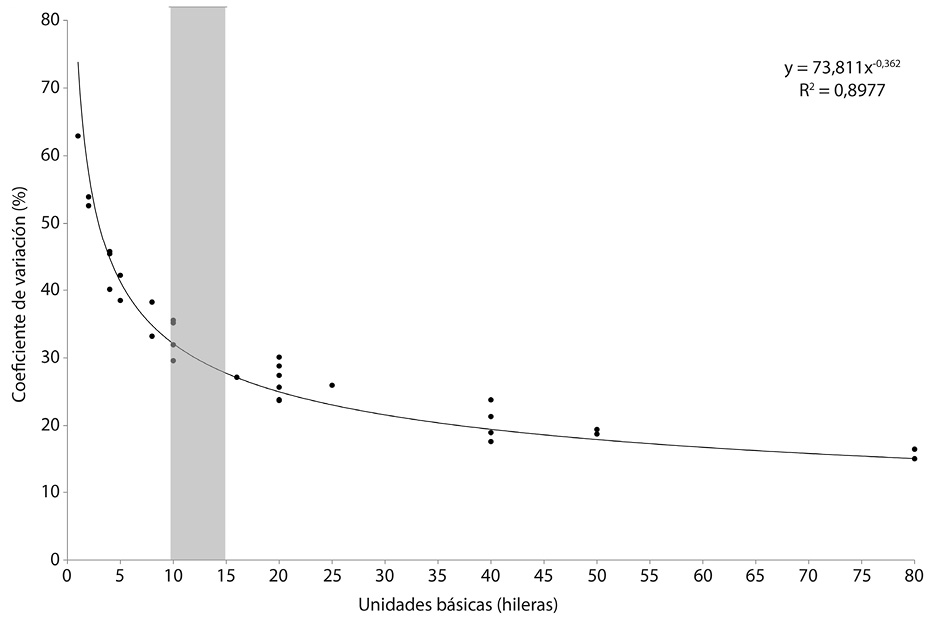
Con los datos que se muestran en el cuadro 1 se construyó un gráfico de dispersión (Fig. 1) donde los puntos colocados en la abscisa fueron los correspondientes al número de unidades básicas, mientras que los puntos colocados en la ordenada fueron los correspondientes a los coeficientes de variación para cada tamaño. Se omitieron los tamaños superiores a 80 unidades básicas para poder apreciar mejor el comportamiento de la curva.
El gráfico resultante es una curva que cae abruptamente al principio y luego se convierte en una línea casi paralela al eje de las X, lo que es un resultado típico de los ensayos de uniformidad utilizados para determinar un tamaño óptimo de unidad experimental (Alvarez et al.1986). A este método se le denomina curvatura máxima y ha sido utilizado en diversos cultivos para estimar el tamaño óptimo de unidad experimental (Kavitha, 2010). Se utilizó una línea de mejor ajuste de tipo potencial, ya que es la línea de tendencia que mejor se ajusta al conjunto de datos, con un R2 de 89,77% (para este cálculo si se tomaron en cuenta los tamaños que se omitieron en el gráfico). Esto quiere decir que el tamaño de parcela explica en un 89,77% la variabilidad en el coeficiente de variación.
Según lo establece la metodología, el punto de la curva, donde un aumento de unidad experimental no genera un cambio significativo en el coeficiente de variación, es donde se encuentra el tamaño óptimo de unidad experimental y se establece por inspección visual de la curva (Mamani, 1971; Alvarez et al.1986; Ferreira et al. 2009). Sin embargo, varios autores señalan que este método posee una gran desventaja, ya que establecer el punto de curvatura máxima mediante inspección visual puede generar cierto grado de error debido a subjetividad y además, va a depender en alto grado de la escala del gráfico que se examine (Mamani, 1971; Ferreira et al., 2009).
En la Figura 1 se observa que en el ámbito de 12 a 16 unidades básicas, se encuentra la región donde la curva deja de caer abruptamente y adquiere un comportamiento casi constante, es decir, que en algún punto de esa región es donde se encuentra el tamaño óptimo de unidad experimental, expresado en número de unidades básicas.
Primera derivada: Para realizar una selección más objetiva del tamaño de unidad experimental se derivó la función de la ecuación de regresión y se igualó a menos uno. Como se muestra a continuación:
y = 73,81x-0,362 Ec. 2
y’ = -26,71x-1,362 Ec. 3
-26,71x-1,362 = -1 Ec. 4
Sí se despeja de la ecuación 4 el valor de x, se obtiene que este es 11,16 (para efectos prácticos, 12), o sea, que ese es el punto en donde al incrementar en una unidad básica el tamaño de unidad experimental el coeficiente de variación de reduce en 1% por lo que aumentar el tamaño más allá de este punto ya no tiene efecto significativo en la precisión. De esta manera se obtiene el punto de curvatura máxima de una manera objetiva y se evita la subjetividad de la interpretación visual.
Forma de unidad experimental: La prueba de Levene determinó que no existen diferencias significativas (p=0,675) entre las variancias de las formas que se pueden generar a partir de un mismo tamaño.
Heterogeneidad del suelo: En el trópico, a diferencia de otras latitudes, uno de los principales problemas que se presenta en experimentación agrícola es la heterogeneidad del suelo, esta es muy variable en espacios de terreno relativamente pequeños. Dicha variabilidad es un problema común para los investigadores agrícolas, lo que obliga al experimentador a buscar un tamaño y una forma adecuados de unidad experimental que logre encerrar toda la variabilidad presente en el suelo, de manera que la única variabilidad que se exprese entre parcelas sea producto de los tratamientos que se aplican (Asif & Anver, 2003).
Gomez y Gomez (1984) señalan que la caracterización adecuada de la heterogeneidad del suelo en el sitio experimental es una buena guía para la escogencia de un tamaño adecuado de unidad experimental.
Por la naturaleza del ensayo de uniformidad todas las fuentes de variación a excepción de la variación del suelo se mantienen constantes, por lo que es esta heterogeneidad del suelo la que explica la variación de la producción de una unidad básica a otra, a mayor variabilidad en la producción entre unidades básicas mayor variabilidad del suelo y viceversa, lo que provee una idea de la heterogeneidad del suelo en el sitio del experimento, factor que está directamente relacionado con la definición de un tamaño adecuado de unidad experimental (Gomez & Gomez, 1984).
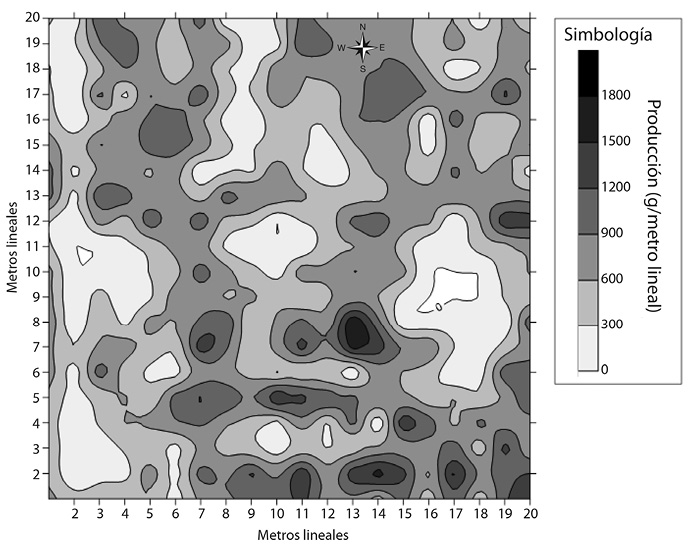
Con el programa de cómputo Golden Software Surfer© se construyó un mapa de contorno (Fig. 2) para lo cual se utilizó la variable producción en gramos.
En la Figura 2 se observa como varió la producción dentro del sitio del ensayo, donde los colores más claros están asociados a producciones menores y los más oscuros a producciones mayores. Esta variabilidad en la producción se relacionó con una variabilidad en el suelo del sitio experimental puesto que todos los demás factores generadores frecuentes de variabilidad en un ensayo se mantuvieron constantes, según especifica la técnica del ensayo blanco.
Índice de Smith para medir la heterogeneidad del suelo: El mapa de contorno si bien proporciona una idea de la variabilidad del sitio no provee de un valor con el cual se pueda cuantificar dicha variabilidad. Por lo que se calculó el índice de Smith.
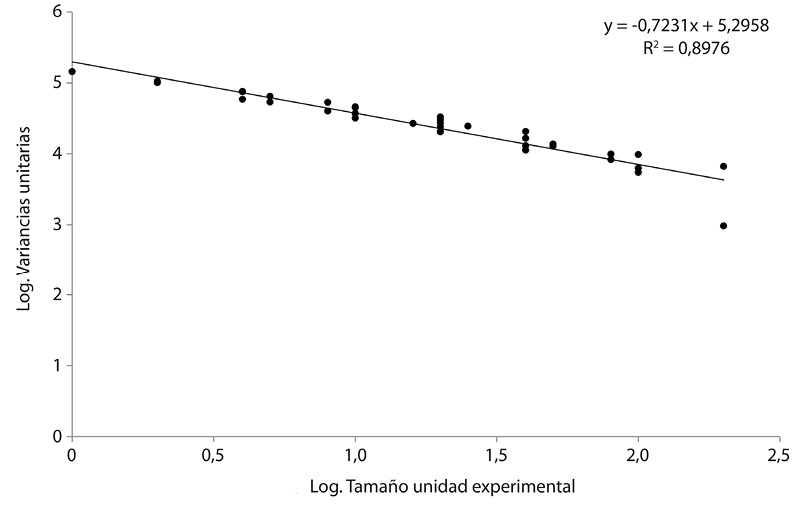
La regresión entre los logaritmos de los tamaños de parcela contra los logaritmos de las variancias unitarias derivó en el siguiente gráfico (Fig. 3).
Según el método propuesto por Smith (1938), la pendiente de la ecuación de la recta (“b”) correspondiente al gráfico anterior (Fig. 3) es el índice de Smith para la heterogeneidad del suelo (Barrientos, 1981), para este caso dicho valor fue de: 0,72.
El valor de la pendiente en este tipo de relaciones inversas, siempre va a tomar valores negativos, sin embargo, el signo es una indicación de la dirección de la regresión entre las variables relacionadas y el valor de la pendiente indica la intensidad de esta relación (Moya, 2009). El índice de Smith para su correcta interpretación debe tomar valores entre 0 y 1 porque omite el signo y toma en cuenta únicamente el valor absoluto de la correlación (Barrientos, 1981; Mayor et al., 2012).
Sin embargo, Federer (1963) mencionado por Mayor et al. (2012), recomienda estimar el coeficiente de heterogeneidad del suelo de manera que se ponderen los logaritmos de las variancias unitarias por sus respectivos grados de libertad. Para calcular el coeficiente de heterogeneidad del suelo ponderado se utilizó la siguiente ecuación:
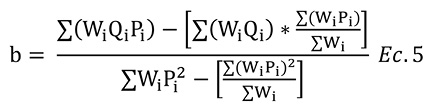
Donde:
Qi= logaritmo de la varianza unitaria
Pi= logaritmo del tamaño de unidad experimental
Wi= grados de libertad correspondientes a cada varianza (número de parcelas de tamaño Xi-1)
Como se mencionó anteriormente, el índice de Smith puede tomar valores entre 0 y 1 donde valores cercanos a 0 indican que el suelo es homogéneo, mientras que valores cercanos a 1 indican suelos heterogéneos; mayoritariamente los valores de este índice se encuentran en un ámbito de 0,20 y 0,90 (Centro Internacional de Agricultura Tropical, 1982; Gomez & Gomez, 1984). Una vez aplicada la fórmula (Ec. 5) se obtuvo que el valor ponderado correspondiente al índice de Smith es de 0,62, lo que indica que el suelo donde se ejecutó el experimento es heterogéneo y respalda la variabilidad que muestra el mapa de contorno (Fig. 2).
DISCUSIÓN
Hasta que se efectuó este trabajo no existía información acerca del tamaño de unidad experimental para ensayos de rendimiento con maíz en la zona de Santa Cruz, Guanacaste.
Tamaño adecuado: El tamaño que aquí se define corresponde al tamaño de parcela útil y no al de parcela total. Por lo que a este tamaño se le deben agregar los bordes que se consideren necesarios según sean las necesidades del ensayo.
El tamaño adecuado de unidad experimental se encontró en el ámbito de 12 a 16 unidades básicas. Párraga y Chacín (2000b) estimaron, con el método de curvatura máxima, que el tamaño de parcela en maíz para la variable rendimiento se encontraba entre 7 y 13 unidades básicas. Además calcularon el índice de Smith, obtuvieron valores 0,61 y 0,53 para el índice sin ponderar y ponderado, respectivamente.
El rango que encontraron estos autores es inferior al que se encontró en este trabajo, esto podría explicarse por el índice de Smith. En el trabajo de Párraga y Chacín (2000b) el índice de Smith ponderado fue de 0,53, mientras que en este trabajo el índice de Smith ponderado fue de 0,62 lo que indica un suelo más heterogéneo.
Monzón (1956) recomendó como tamaño de unidad experimental una parcela de 12 unidades básicas, sin embargo, este autor no provee información acerca del índice de heterogeneidad del suelo.
Si bien, en esta pesquisa se define 12 unidades básicas como tamaño adecuado de unidad experimental, no se pueden descartar otros tamaños cercanos a este punto. Las dimensiones de unidad experimental están condicionadas en gran medida por la heterogeneidad del suelo (Bueso, 1985), al ser esta cuantificable mediante el índice de Smith, es posible realizar comparaciones entre diferentes áreas experimentales (Centro Internacional de Agricultura Tropical, 1982), así pues, en un sitio experimental donde el suelo sea más uniforme que en donde se efectuó este trabajo se podría utilizar un tamaño de unidad experimental más pequeño -por ejemplo de 10 unidades básicas - o si por el contrario se está trabajando en un suelo con mayor grado de heterogeneidad o se quiere trabajar con mayor grado de precisión se puede hacer uso de una unidad experimental de mayor tamaño.
No es que se está haciendo caso omiso al punto de curvatura máxima definido por la primera derivada, sino es que se está tomando como punto de referencia. Es permisible seleccionar tamaños cercanos al óptimo según las condiciones bajo las que se trabaje (Barrientos, 1981).
Forma de la unidad experimental: Se propuso 12 unidades básicas como tamaño adecuado de unidad experimental empero hay que definir cómo distribuir esas unidades básicas en el campo.
Los surcos dentro del lote del experimento estuvieron ubicados de norte a sur. Entonces por aspectos prácticos las posibles unidades experimentales que se puedan ubicar de oeste a este no se toman en cuenta. Esto deja únicamente las siguientes opciones, en largo (metros lineales de un mismo surco) x ancho (número de surcos): 3 x 4; 4 x 3; 6 x 2; 2 x 6; 12 x 1 y 1 x 12 como posibles formas para un tamaño de 12 unidades básicas.
Debido a que el resultado de la prueba de Levene arrojó que no había diferencia entre las variancias de estas formas, en teoría se podría utilizar cualquiera de las combinaciones mencionadas. No obstante, Calero (1965), Mamani (1971), Escobar (1981) y Párraga (2000), entre otros autores afirman que la mayor eficiencia en un ensayo se logra con parcelas largas y angostas. La parcela útil de dos surcos de seis metros de largo podría ser una buena elección, en términos de eficiencia, para una unidad experimental de 12 unidades básicas.
Aumento en la precisión y ahorro de recursos: Si bien el sitio donde se realizó este ensayo blanco es heterogéneo si se utiliza un tamaño de unidad experimental de 12 unidades básicas se puede abarcar toda la variabilidad del suelo, lo que contribuye con la precisión y la confiabilidad del ensayo sin necesidad de utilizar tamaños superiores.
En los diferentes tipos de ensayos que se realizan en maíz, donde se puede evaluar materiales promisorios, herbicidas, fungicidas, fertilizantes, insecticidas o cualquier otra práctica de manejo, uno de los recursos más costosos que se utiliza es la semilla, que inclusive, en algunas ocasiones es un recurso limitante, debido a su baja disponibilidad, por lo que un uso eficiente de este insumo es necesario. Por consiguiente, si se hace uso de una parcela de tamaño mayor al necesario se va a incurrir en un gasto mayor del tanto del insumo que se evalúa, como de otros insumos que se deben emplear y de la mano de obra; lo que eleva los costos de experimentación, que de por sí ya son elevados (Centro Internacional de Agricultura Tropical, 1982).
Este ahorro de recursos que deriva de la utilización de un tamaño y una forma de unidad experimental adecuados podría traer repercusiones importantes en todo el proceso de investigación. Un aumento en la precisión no solo se lograría debido a la utilización de un tamaño adecuado de parcela, sino también que al existir un ahorro importante de recursos las compañías o empresas que realizan investigación en maíz podrían utilizar estos recursos extra para aumentar el número de repeticiones de la prueba de interés, lo que daría mayor confiabilidad a los resultados obtenidos, Mamani (1971) menciona que un aumento en el número de repeticiones tienen un mayor efecto sobre la disminución del error experimental en una prueba crítica que aumentar el tamaño de parcela.
REFERENCIAS
Álvarez, R., Soto, M., & Gómez, H. (1986). Tamaño de parcela y número de repeticiones para estimar una población de Spodoptera frugiperda (Smith) y su daño en maíz. Revista Facultad Nacional de Agronomía, 39(2), 6-16.
Asif, M., & Anver, M. (2003). Variability in fields experiments in maize crop in Pakistan. Pakistan Journal of Agriculture Science, 40(3-4), 207-2.
Barrientos García, M. (1981). Evaluación de 4 métodos para la determinación de tamaño y forma óptimos de parcela para experimentación agrícola. (Tesis inédita de licenciatura). Universidad de San Carlos, San Carlos, Guatemala. 79 p.
Barros, I., & Tavares, M. (1995). Estimativa do tamaño ótimo de parcelas experimentais através de cálculos algébricos. Revista Bragantia, 54(1), 209-215.
Box, G., Stuart, J., & Hunter, W. (2008). Estadística para investigadores: diseño, innovación y descubrimiento. Barcelona, España: Reverté.
Bueso Campos, M. (1985). Determinación del tamaño óptimo de parcela experimental en melón (Cucumis melo) para el departamento de Chiquimula, y en tomate (Lycorpesicum esculentum) para el valle de La Fragua, Zacapa. (Tesis inédita de licenciatura). Universidad de San Carlos, San Carlos, Guatemala. 33 p.
Calero Hidalgo, E. (1965). Estudio del tamaño y forma de la parcela experimental para ensayos de campo en frijol (Phaseolus vulgaris L.). (Tesis inédita de maestría). CATIE, Turrialba, Costa Rica. 36 p.
Centro Internacional de Agricultura Tropical. (1982). La heterogeneidad del suelo y los ensayos de uniformidad: guía de estudio para ser usada como complemento de la Unidad Audio tutorial sobre el mismo tema. CIAT, Colombia. 24 p.
Chacín, F. 1977. Tamaño de parcela experimental y su forma. Revista de la Facultad de Agronomía (Maracay, Universidad Central de Venezuela), 9(3), 55-74.
Custódio Silva da, W. (2010). Comparacao de métodos para estimar o tamaño ótimo de parcela embananeira. (Tesis inédita de maestría). Universidad Federal de Vicosa, Vicosa, Brasil. 37 p.
Escobar, C. (1981). Estimación del tamaño óptimo de parcela experimental para ensayos de rendimiento con maíz. Revista Facultad Nacional de Agronomía Medellín, 34(1), 31-36.
Escobar, C., Buitrago de, & I., Jaramillo, J. (1990). Tamaño de parcela experimental y número de repeticiones para ensayos de rendimiento con Caupi, Vignaungiculata (L) Walp. Revista Facultad Nacional de Agronomía de Medellín, 43(1), 73-91.
Ferreira, P., Furtado, D., & Ramalho, A. (2009). Tamanho ótimo de parcelas experimentais: proposicao de metodos de estimacao. Revista Brasileira de Biometria, 27(2), 255-268.
Gomez, K. (1972). Techiques for field experiments with rice. International Rice Research Institute, Philippines: John Wiley&Sons
Gomez, K., & Gomez, A. 1984. Statistical procedures for agricultural research. 2da ed. Philippines: John Wiley&Sons.
Instituto Meteorológico Nacional. (2011) Datos meteorológicos de Liberia y Santa Cruz 2007-2010, Guanacaste. 10p.
Kavitha, B. (2010). Study on optimum plot size and optimum plot shape of soybean crop. (Tesis inédita de maestría). University of Agricultural Sciences, Dharwad, India. 58 p.
Mamani, L. (1971). Determinación del tamaño, forma y repetición de la parcela para ensayos de rendimientos en frijol (Phaseolusvulagirs L.). (Tesis inédita de maestría). CATIE, Turrialba, Costa Rica. 83 p.
Mayor, V., Blair, M., & Muñoz, J. (2012). Metodología para estimar el coeficiente de heterogeneidad del suelo, el número de repeticiones y el tamaño de parcela en investigaciones con frijol (Phaseolus vulgaris L.). Acta agronómica, 61(1), 32-39.
Monzón, D. (1951). Análisis e interpretación de un ensayo de uniformidad con maíz. Agronomía Tropical, 6(1), 15-22.
Moya, L. (2009). Introducción a la estadística de la salud. Costa Rica: Editorial UCR.
Oliveira, Sérgio de., Storck, L., Lopes, S., Lúcio, A., Feijó, S., & Damo, H. (2005). Plot size and experimental unit relationship in exploratory experiments. Scientia Agricola, 62(6), 585-589.
Párraga, C., & Chacín, F. (2000a). Comparación de metodologías univariadas en la determinación de unidades experimentales de campo: renglón maíz (Zea mays L.). Revista Facultad de Agronomía de Maracay, 26(1), 175-190.
Párraga, C., & Chacín, F. (2000b). Métodos multivariados para determinar el número de réplicas, la forma y el tamaño óptimo de unidad experimental en el cultivo de maíz (Zea mays L.). Revista de la Facultad de Agronomía de Maracay, 26(1), 163-173.
Rosselló, J. M., & Fernández, M. (1986). Guía técnica para ensayos de variedades de campo. FAO. 144 p.
Rodríguez, N., Sánchez, H., & Pacheco, P. (1993). Determinación de tamaño y forma óptimos de parcela para ensayos de rendimiento con café. Revista Colombiana de Estadística, 14(27), 50-64.
Sánchez, M., Mejía, A., Villanueva, C., Castellanos, J., Sánchez, C., & Jiménez, C. (2006). Determinación del tamaño adecuado de parcela experimental en calabaza pipiana (Cucurbita argyrosperma hubervar. Stenosperma). Revista Fitotecnia Mexicana, 29(004), 339-348.
Santos, D., Machado, F., Dal’Col, A., Storck, L., & Cargnelutti, F. (2012). Plot size for the green beans crop. Revista Ciencia Agronómica, 43(1), 119-128.
Smith, F. (1938). An empirical law describing heterogeneity in the yields of agricultural crops. Journal of Agriculture Science, 28(1), 1-23.
Vallejo, R., & Mendoza, H. (1992). Plot technique studies on sweet potato yield trials. Journal of the American Society for Horticultural Science, 117(3), 508-511.