El balance hídrico del suelo se basa en el principio de la conservación de la masa, donde toda el agua que entra al suelo debe ser igual a la cantidad de agua que se almacena más el agua que sale de él. Las entradas al sistema son debidas a la precipitación que se infiltra del agua hacia el suelo y las salidas se deben a la evapotranspiración y la descarga hacia los acuíferos (Fetter, 2001). Los factores que influyen en el balance hídrico del suelo son parámetros meteorológicos (precipitación, temperatura, horas de sol, etc.), geográficas (uso del suelo y pendiente) y geológicas (textura del suelo, velocidad de infiltración).
Según Parr y Bertrand (1960), la tasa de infiltración es gobernada solamente por la masa del suelo y es en gran parte, independiente de las condiciones superficiales. En contraste, Horton (1940) indicó que la tasa de infiltración es gobernada principalmente por las condiciones cerca de la superficie del suelo.El proceso de infiltración de agua en el suelo ha sido intensamente estudiado debido a su importancia en el manejo del agua en la agricultura, la conservación del recurso suelo, la recarga hacia los acuíferos y otras actividades técnicas. La velocidad de infiltración determina la cantidad de agua de escurrimiento superficial y con ello el peligro de erosión hídrica. En casi todos los métodos de riego la velocidad de entrada de agua al suelo determina los tiempos de riego y los diseños de los sistemas en cuanto al tamaño de las unidades superficiales y los caudales a utilizar.
Además, el proceso de infiltración es de gran importancia práctica dado que su velocidad determina generalmente la cantidad de agua de escurrimiento, pudiendo detectarse así el peligro de erosión durante inundaciones o lluvias muy intensas. En los casos en que la velocidad de infiltración es limitada puede ser afectado todo el sistema de economía de agua de la zona de enraizamiento; para un manejo eficiente del suelo y del agua se requiere un conocimiento detallado del proceso de infiltración, debido a que éste se correlaciona con las propiedades del suelo y con el aporte de agua al sistema (Gurovich, 1985).
La ecuación de Green y Ampt (1911) es una simplificación de la ecuación de Richards, que a su vez proviene de una combinación de la ecuación de Darcy y la ecuación de continuidad (Chow, 1959). Esta ecuación simplifica las condiciones iniciales y de contorno del problema, asume suelo profundo y homogéneo, con contenido de humedad inicial uniforme en profundidad, asumiendo que el movimiento de agua se produce en forma de frente con la misma velocidad en toda la sección transversal del suelo (flujo tipo pistón).
Kostiakov (1932) propuso una ecuación empírica que ha demostrado una gran aceptación para ser utilizadas en las prácticas de riego. A pesar de que las unidades y dimensiones de los parámetros C y α parecen no tener significado, si se pueden interpretar físicamente. El parámetro C representa la lámina de agua infiltrada durante el primer minuto y depende de la estructura y de las condiciones que tiene el suelo al inicio de la aplicación del agua.
El parámetro α es un indicativo de que cómo la tasa de infiltración decrece con el tiempo de aplicación del agua y por consiguiente, depende de los cambios que puedan ocurrir en la estructura del suelo como efecto del humedecimiento (Steer& Rodríguez, 2008). El modelo de Kostiakov está representado por la ecuación:
i = C t α
Cuando se deriva esta ecuación se obtiene la velocidad de infiltración o infiltración instantánea que está dada en cm/hr, así: i = C t-α
Exploramos las tres metodologías comúnmente utilizadas para determinar la velocidad de infiltración que es un parámetro necesario para realizar el cálculo del balance hídrico. Presentamos el caso de la cuenca del río Suquiapa, donde el resto de parámetros necesarios para el balance se mantienen constantes y se variará únicamente el valor de la velocidad de infiltración obtenida por alguno de los tres métodos empleados en el campo: doble anillo, permeámetro de Guelph o Porchet.
MÉTODOS
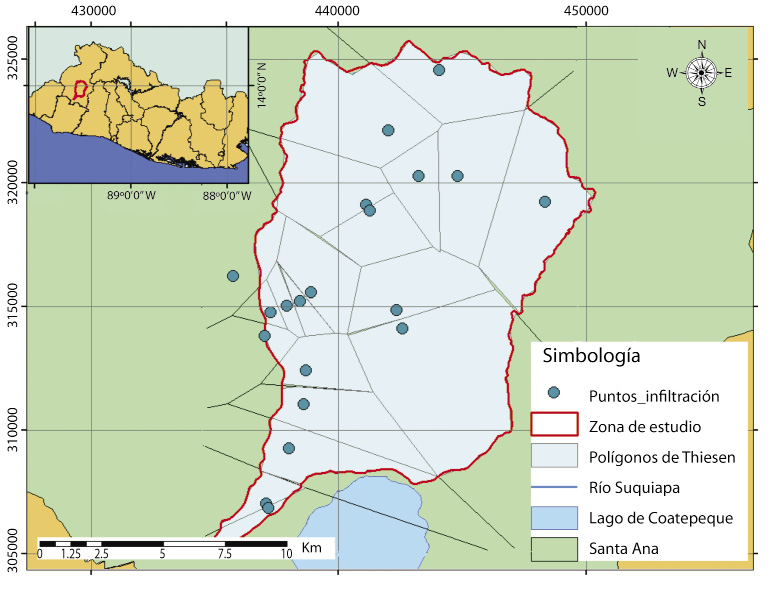
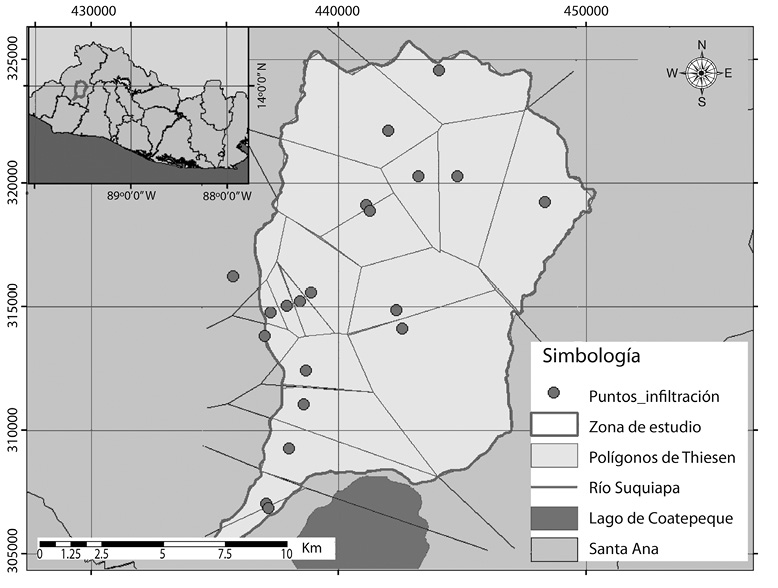
El área de la cuenca del río Suquiapa fue dividida en polígonos de Thiessen (Fetter, 2001, 1994) siguiendo los métodos propuestos para el balance hídrico de suelos de Schosinsky (2006), los cuales son ampliamente utilizados en todo Centroamérica y de uso obligatorio en Costa Rica (La Gaceta, 2010). Siguiendo estos métodos se calcula la recarga potencial al acuífero para un año promedio (con una discretización temporal mensual).
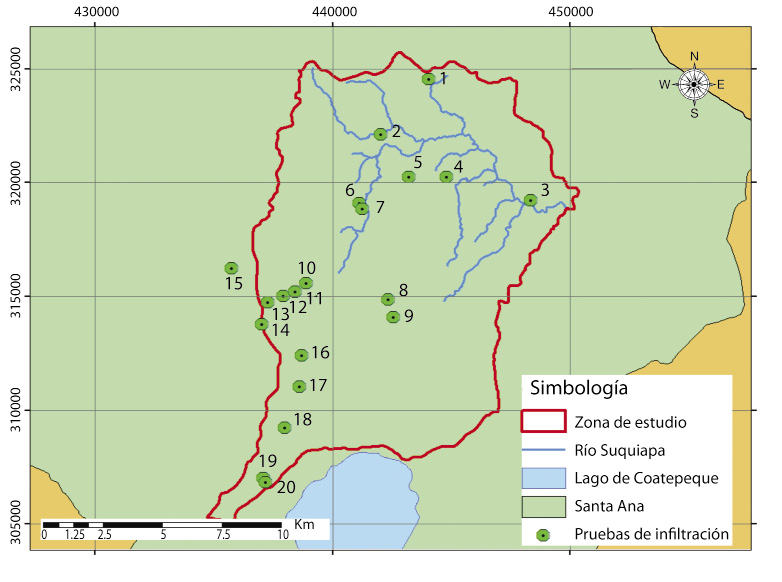
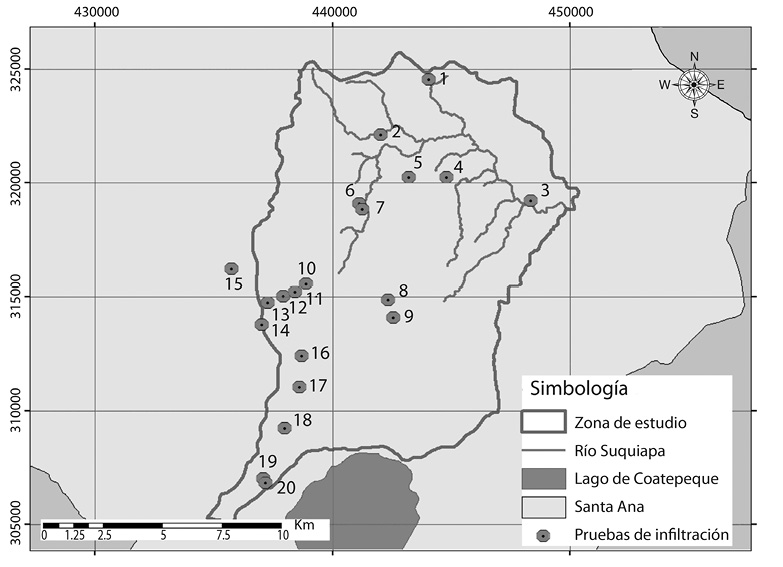
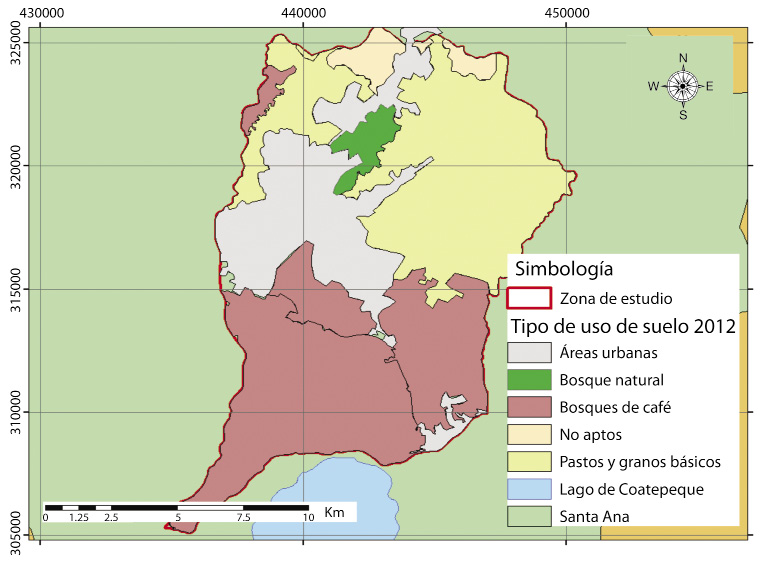
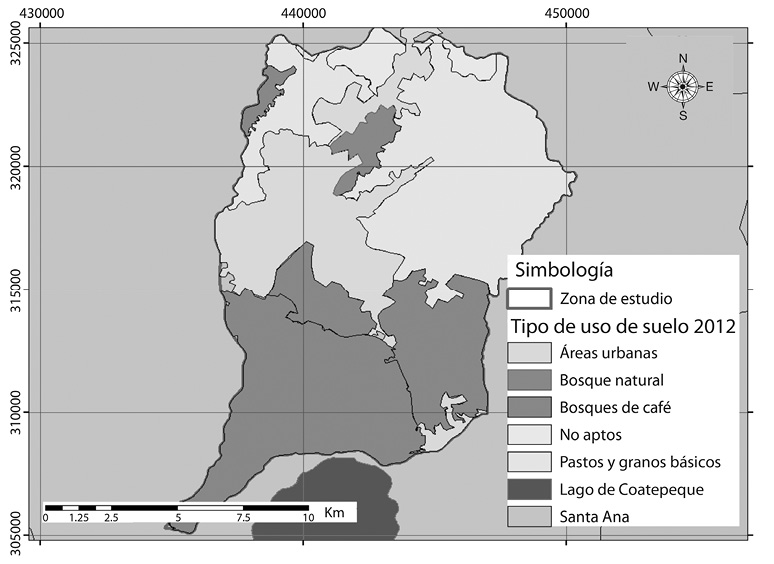
Escogimos 3 de los métodos más utilizados para la determinación de la velocidad de infiltración en el campo y los aplicamos en 20 puntos seleccionados de la cuenca, los sitios los escogidos en función del tipo de uso de suelo (Fig. 1).
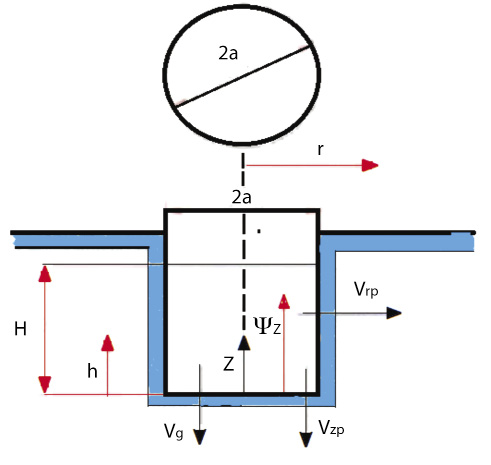
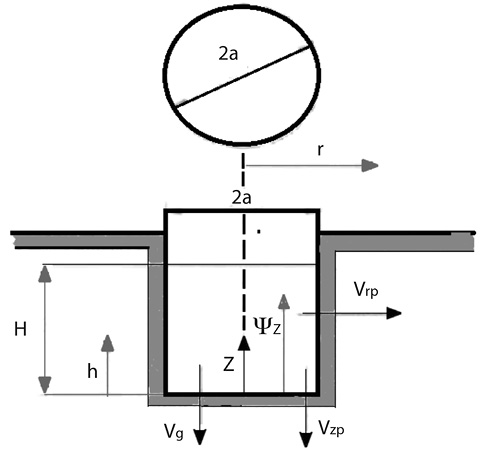
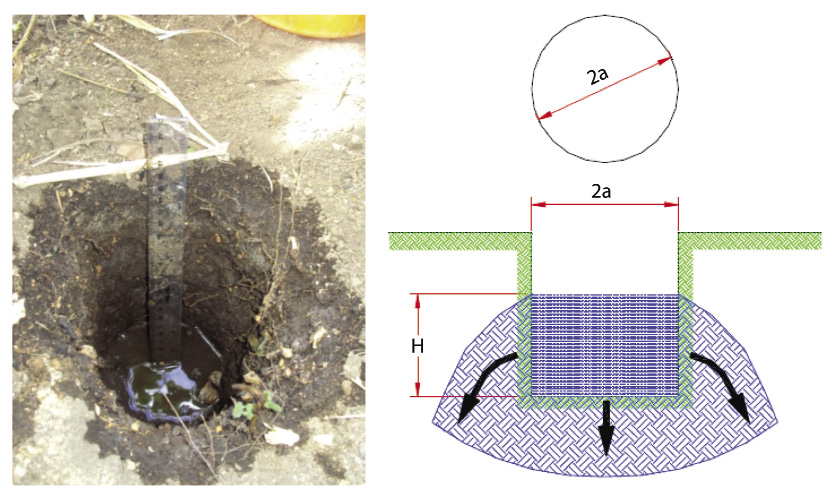
Método del permeámetro de Guelph: es una modificación del permeámetro presentado por Talsma y Hallam (1980). Este permeámetro consiste en un Mariotte construido con dos tubos intrínsecos que actúan como depósito manteniendo la carga hidráulica constante en un hoyo practicado en el suelo. Determinando el valor de conductividad hidráulica saturada en campo por medio de un procedimiento numérico, a partir de mediciones de velocidad de flujo infiltrándose en estado estacionario.Los modelos analíticos que representan el flujo a través de un pozo o agujero de infiltración en régimen permanente desde un pozo de radio a y altura de agua constante “H”, en un medio poroso, rígido, semi-infinito, homogéneo e isotrópico, se deducen a partir de la ley de Darcy, ya sea en un suelo totalmente saturado o no, considerando que pueden intervenir distintos tipos de flujo (Fig. 2).
A partir de la figura 2 se puede deducir que:
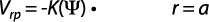

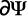
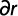
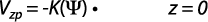

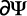
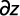
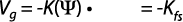
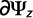
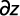

Luego el caudal infiltrado en el agujero se puede escribir como:
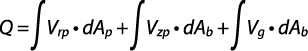
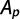
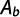
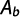
Desarrollando de manera teórica, numérica y empírica la ecuación anterior, se puede obtener la siguiente expresión para el caudal de infiltración:


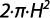


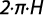


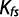
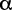
Los dos primeros términos de la ecuación anterior representan el flujo de agua a través del fondo y de las paredes del pozo debido al gradiente de presión. El primero considera el flujo en condiciones saturadas y el segundo considera el efecto de la zona no saturada que rodea el pozo. El tercer término se refiere al flujo gravitacional.Reynolds & Elrick (1986), recomiendan expresar el factor C mediante una solución numérica que se expresa como:
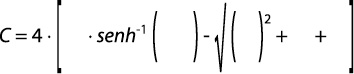



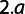
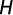






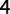


Según Prieto, et al. (2006) el permeámetro de Guelph presenta menor variabilidad en comparación a los infiltrómetros de doble anillo e indican que con menor número de pruebas se llega a resultados representativos de un área de terreno. Además, las pruebas se realizan en menor tiempo y con menor número de operarios, por lo que se puede concluir que este método resulta más práctico, y menos costoso que el método de infiltrómetro de anillo.
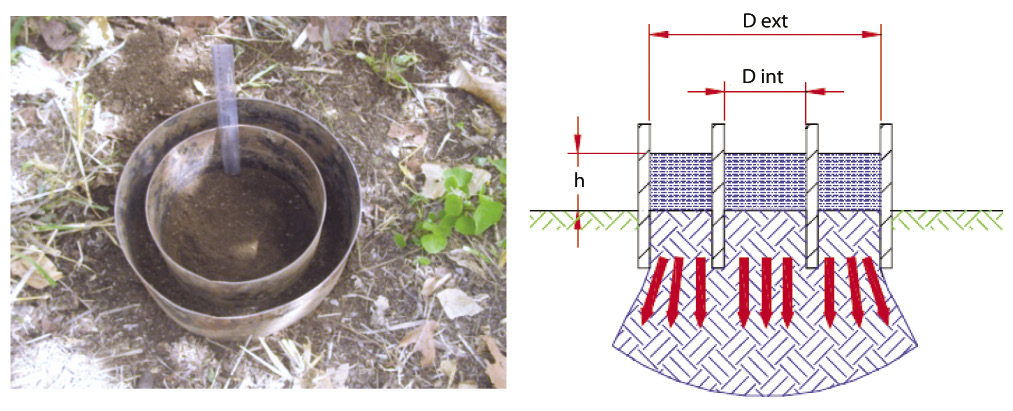
Método de doble anillo: según Selker et al. (1999), el método del doble anillo es la prueba más común para la estimación de propiedades hidráulicas del suelo. Horton (1939), estableció, para el caso de un suelo sometido a una precipitación con intensidad siempre superior a la capacidad de infiltración, una relación empírica para representar el declive de la infiltración con el tiempo puede ser presentada de la siguiente forma:
It = Ib + (Ii - Ib) e(-kt)
La tasa mínima de infiltración Ib teóricamente sería igual a la conductividad hidráulica saturada Ksat, si no hubiese el efecto del aire comprimido en el interior del suelo, dificultando la infiltración. Por eso Ib es normalmente menor que Ksat.
El ajuste de la ecuación de Horton a datos medidos en campo permite la determinación de los parámetros Ii ,Ib y k. El parámetro Ib es fácilmente identificable en los experimentos, porque representa la conductividad hidráulica saturada aparente del suelo (aparente porque incluye la resistencia proporcionada por el aire comprimido en los poros del suelo natural). El parámetro Ii también es obtenido inmediatamente de los experimentos porque es una tasa de infiltración inicial, esto es una tasa de infiltración en el momento en que es alcanzada la saturación superficial y comienza a haber escurrimiento (exceso) superficial, lo que equivale a decir que Ii es igual a la intensidad de la precipitación que saturó la superficie del suelo. Establecidos Ib e Ii resta apenas determinar el parámetro k, lo que es hecho a través del ajuste de la ecuación anterior a los puntos I y t medidos en campo (Nave et al., 1994). Integrando la ecuación anterior con respecto al tiempo, se obtiene la ecuación de los volúmenes infiltrados acumulados en el tiempo:
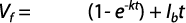
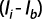
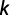

De acuerdo con la norma ASTM D3385-94, el intervalo de velocidad de infiltración para el cual es válida esta prueba es entre 1x10-6 cm/s a 1x10-2 cm/s.
Para su determinación los dos anillos (exterior e interior) se introducen en el suelo a una profundidad de 10 a 15 cm, hasta lograr que estén perfectamente enterrados y nivelados. El espacio interno de los anillos se llena de agua. Existen dos tipos básicos de pruebas: carga constante o carga variable. En esta investigación se utilizó el caso de carga variable, en el que se permite que el nivel del agua descienda a lo largo de la prueba (Fig. 3). El método consiste en tomar lecturas del descenso del nivel de agua en el anillo interior. Cuando se consigue que la tasa de la infiltración sea constante, la prueba se termina. Se puede demostrar aplicando la ecuación de Darcy que el valor obtenido de la infiltración básica es igual a la conductividad hidráulica saturada si la filtración es estrictamente vertical y el perfil del suelo es profundo y uniforme (Coello, 2005.)
El postulado de Horton establece que la curva que representa la capacidad de infiltración se manifiesta de esa manera, solo si la intensidad de precipitación es mayor que la capacidad de infiltración del suelo analizado. Este principio o postulado es debidamente respetado en el ensayo de infiltración de doble anillo, porque siempre hay agua en superficie que satisface la capacidad de absorción que tiene el suelo en su grado máximo o potencial, cualquiera sea el tiempo que transcurre desde el inicio del ensayo.
Kostiakov (1932) propuso un modelo exponencial, el cual desarrollo de manera empírica, como se muestra en la siguiente ecuación:
f = atb
Para t -> ∞ f = fbásica
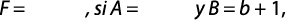
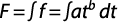
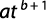
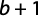

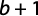


Entonces
F = AtB
Donde:
Entonces linealizando la ecuación anterior:
Ecuación de una recta:
Y = log (F), Ao = log (a), B = B, X = log (t)
Donde:
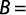

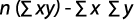
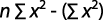
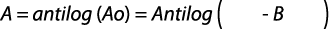
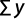
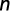

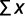
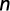

Coeficiente de determinación:
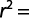

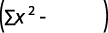
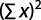
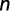

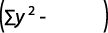
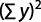
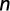

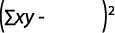

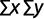
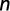
Método de Porchet: consiste en un agujero cilíndrico, excavado en tierra, de radio y profundidad constante, en el cual se mide el descenso del nivel del agua dentro del pozo a través del tiempo (Figura 4) (Kessler y Oosterbaan, 1977). Una vez alcanzada la saturación del terreno adyacente al pozo, la velocidad de infiltración será casi constante. Bajo estas condiciones, suponiendo conductividad hidráulica constante y aplicando la ley de Darcy, la infiltración total (Q) será igual a:
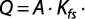

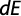
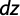
Si se considera que el flujo que ingresa al suelo por el fondo y las paredes escurre con gradiente hidráulico unitario, la expresión queda reducida a:
Q = A . Kfs
Como el agua se infiltra tanto por las paredes como por el fondo del pozo, el área total de infiltración en un instante cualquiera ti es:
A(ti) = 2 . p . a . H(ti) + p . r2
Donde A (ti) es la superficie sobre la cual se infiltra el agua en el suelo en el tiempo ti [L2], a es el radio del pozo [L] y H (ti) es el nivel del agua en el pozo en el tiempo ti [L] y el caudal se expresa entonces por:
Q(ti) = 2 . Kfs . p . a . (H(ti) +



)
Por otro lado, si durante el intérvalo de tiempo dt el nivel de agua desciende una altura dH, la cantidad de agua infiltrada en el suelo es igual a:
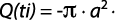
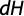
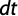

Que integrando entre los límites H1 y H2, igualando con la ecuación 17 y despejando Kfs se obtiene:
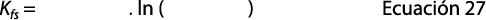

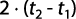


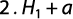
Determinación del balance hídrico de suelos: se busca encontrar la proporción y distribución del agua que recibe el acuífero por infiltración directa de lluvia. Este es un método que analiza la cantidad de agua de lluvia que recarga al acuífero, estableciendo la lluvia que realmente infiltra, una vez que haya pasado los procesos de capacidad de infiltración del suelo y evapotranspiración (ETP).
Con el fin definir la recarga potencial al acuífero, se deben considerar las siguientes variables de la zona de estudio (Schosinsky, 2006):
a. Precipitación, temperatura, brillo solar.
b. Pendientes, uso del suelo (tipo de cobertura vegetal) y velocidad de infiltración.
d. Propiedades físicas del suelo: capacidad de campo, punto de marchitez, densidad aparente.
e. Geología de la zona de estudio.
El cálculo de la recarga potencial y volumen del agua disponible de un acuífero comprende: Recarga Potencial (RP), que comprende la evaluación de la recarga directa por precipitación a través del método del Balance Hídrico de Suelos (BHS) y evaluación de la recarga lateral, ya sea por ríos u otras formaciones geológicas que contengan aguas subterráneas que aporten al sistema analizado.
Balance de Aguas Subterráneas (BAS), éste evalúa la recarga potencial del acuífero en relación con la descarga potencial calculada tanto natural (manantiales y flujo base de ríos) como artificial (bombeo de pozos u otra infraestructura), consiste básicamente en el volumen de agua disponible para su explotación (AD).
RESULTADOS
El cuadro 1 se presentan los valores de velocidad de infiltración (fc), el coeficiente de infiltración (Kfc) y el valor de recarga potencial (Rp) para cada sitio y prueba realizada (Guelph, doble anillo, Porchet). En el caso de los sitios 4 y 9, el ensayo de Porchet no pudo realizarse, por lo que no se tiene un dato para esta prueba en estos puntos.
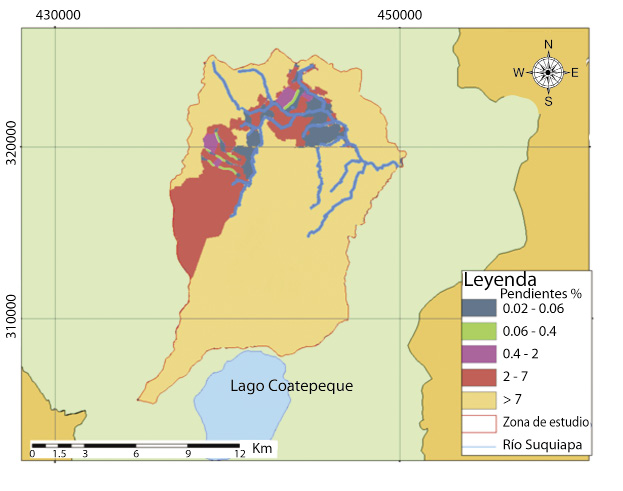
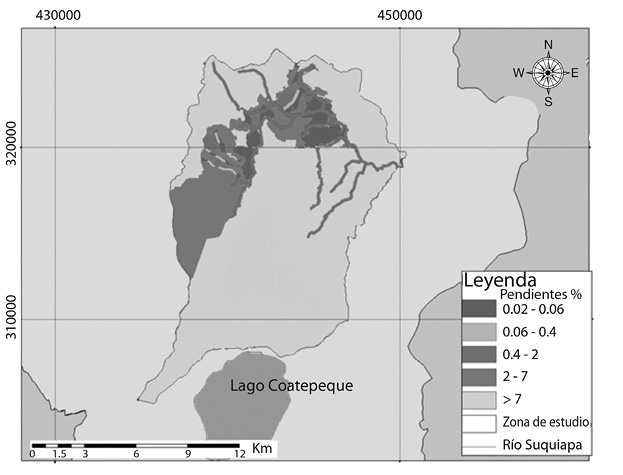
Para el cálculo del balance hídrico de suelos se siguió el método de Schosinsky (2006), para ello se generaron mapas de los distintos parámetros, donde se presentan los de uso de suelo (Fig. 5) y pendientes (Fig. 6).
Escogimos 3 de los métodos más utilizados para la determinación de la conductividad hidráulica en el campo y realizamos pruebas en puntos seleccionados de la cuenca. Presentamos una comparación de los resultados obtenidos de estas pruebas y se comenta sobre las implicaciones que puede tener la escogencia de una de estas pruebas en la realización del balance hídrico de la cuenca. Los tres métodos seleccionados son el método del permeámetro de Guelph, el método del doble anillo y el método de Porchet. Los sitios fueron escogidos en función del tipo de uso de suelos, se realizaron un total de 58 pruebas (Fig. 7).
La conductividad hidráulica (Coello, 2005) saturada es influenciada por las características del suelo y el tamaño de la muestra, cada método de estimación considera factores de suelo diferentes, en casos como el infiltrómetro de doble anillo, y Porchet tienen una fuerte dependencia de los macroporos, grietas y figuras así como de posible actividad de microfauna; el método de carga constante no evalúa dichos factores y considera simplemente la microporosidad.
Cuadro 2
Recarga Potencial para cada uno de
los métodos de infiltración
|
Método de cálculo |
Recarga Potencial (mm) |
Volumen (m3/año) |
|
Guelph |
7 261,39 |
62x106 m3/año |
|
Doble Anillo |
9 309,08 |
80x106 m3/año |
|
Porchet |
9 548,42 |
78x106 m3/año |
Los resultados de la recarga potencial, reflejan que hay una variación significativa dependiendo del método utilizado. Al final de esta investigación es difícil concluir cuál de los métodos es mejor, ya que cada uno tiene sus ventajas y desventajas. Por ejemplo los métodos que requieren menos costos son el de Doble Anillo y Porchet, al contrario el método del Permeametro de Guelph es mucho más caro, pero el consumo de agua es mucho menor que los otros métodos. También, el tiempo requerido para la adquisición de datos es más rápido con el Permeametro de Guelph. Otra característica importante a valorar es el número de operarios que se necesitan, los métodos de carga variable (Porchet y Doble anillo) demandan al menos dos personas, mientras que el de carga constante (Permeametro de Guelph) con uno basta.
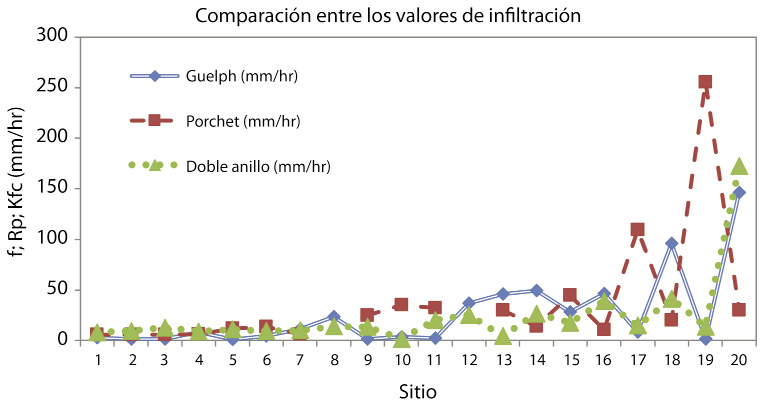
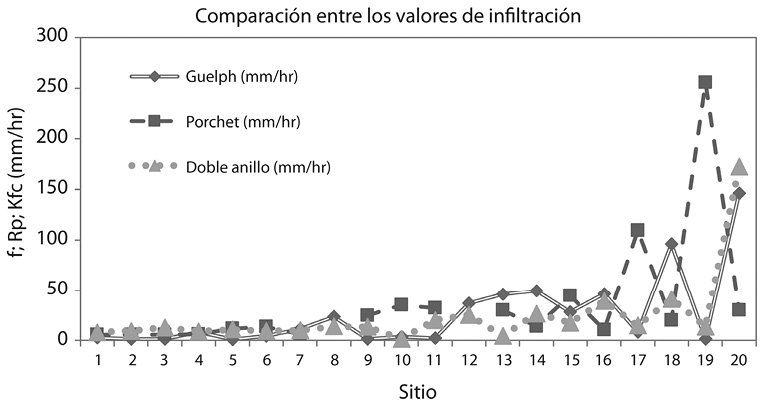
Los tres métodos analizados producen resultados muy similares cuando el resultado está asociado a valores pequeños de tasas de infiltración, mientras que, para valores de tasas de infiltración altos (mayores a 50 mm/hr), los resultados presentan una variación mayor entre los métodos para un mismo sitio (Fig. 8).
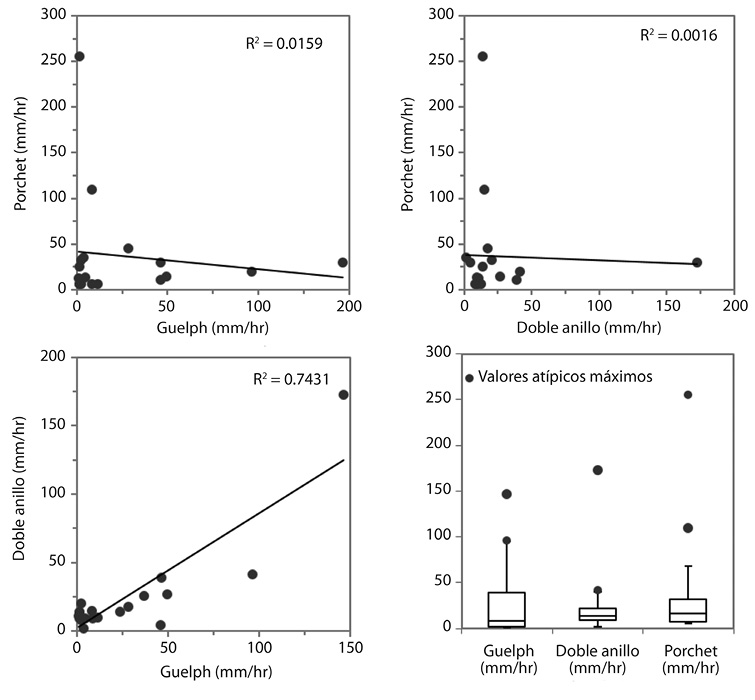
Al comparar entre métodos (Fig. 9), la mejor correlación se observa entre los métodos Guelph y doble anillo (r2=7,4x10-1), mientras que la correlación entre Porchet y Guelph (r2=1,6x10-2) es menor y aún más baja es la correlación entre Porchet y el método del doble anillo (r2=1,6x10-3), El diagrama de caja muestra la información sobre los valores mínimos, máximos, la distribución de los cuartiles 25%, 75% y la ubicación de los valores atípicos; en este diagrama se observa que el método de Porchet obtuvo el valor más alto, se nota además que el permeámetro de Guelph presenta los rangos más amplios de valores y el método del doble anillo tiene la menor variabilidad en general.
Es importante mencionar que debido a que solo se obtuvo una observación por sitio para cada método, no se puede aplicar la técnica de análisis de inferencia estadística, como por ejemplo el ANOVA de Dos Factores, el cual sería el ideal para una correlación analítica de los resultados obtenidos; por lo tanto, se ha realizado un análisis descriptivo de los resultados.
DISCUSIÓN
El método del doble anillo, resultó ser el más difícil de ejecutar en el campo, la media (23,69) obtenida por este método fue la más baja, siendo este uno de los parámetros estadísticos más extendidos, se puede interpretar que la suma de los fc es el menor, también en el gráfico de caja se puede observar que el método de doble anillo tiene los tramos más cortos, es decir, que hay una mayor aglomeración de elementos muestrales, representando una mayor densidad, También la desviación estándar es menor que los otros métodos, Existen varios autores (Gerard-Marchant, 1997, Reynolds y Elrick, 1990, Wu et al., 1999, Youngs et al., 1995) que han desarrollado nuevos modelos analíticos para este método, con lo cual se pueden obtener mejores resultados.
Aunque el método de pozo de nivel variable o Porchet tiene la ventaja de ser muy rápido y fácil de implementar; los resultados de media, mediana, error típico y desviación estándar son los mayores en comparación con los otros métodos; sin embargo, se puede observar en el gráfico 3 que los valores están intermedio de los otros resultados, Es necesario recordar que para obtener un buen resultado en estos métodos de infiltración, es importante saturar adecuadamente el terreno.
Por último, la recarga potencial obtenida por cada método, refleja significativas diferencias, ya que el Permeámetro de Guelph nos conduce al valor más bajo, tal como lo expresa García-Sinovas, et al. (2001). Los valores medios obtenidos con el permeámetro de Guelph fueron inferiores. Reynolds & Elrick, (1986) remarcan que el método del Permeámetro de Guelph está bien fundamentado teóricamente, aunque carece de una verificación de campo, pero que los resultados obtenidos hasta la fecha demuestran que son resultados alentadores. Dafonte, et al., (1999), comprobó que el método del permeámetro de Guelph es una técnica sencilla y rápida, en comparación de otros métodos de cálculo de infiltración. Prieto, (2006) concluye que el método de doble anillo obtuvo valores significativamente mayores que el método de carga constante. Finalizando que el valor de recarga potencial que se obtiene por los métodos de carga variable está influenciado mayormente por los macroporos, por lo que se comprenden que resultara en valores mayores, mientras que el método de permeámetro de Guelph, por lo microporos.
Agradecimiento
Al Servicio Alemán de Intercambio Académico (DAAD) por el financiamiento parcial de esta investigación, a la Universidad de El Salvador (UES), la Universidad de Costa Rica (UCR), Administración Nacional de Acueductos y Alcantarillados (ANDA). El segundo autor agradece el apoyo a través del proyecto 113-B2-A27 de la Vicerrectoría de Investigación de la Universidad de Costa Rica.
REFERENCIAS
ASTM D3385-94. (1994). Standard Test Method for Infiltration Rate of Soils in Field Using Double-Ring Infiltrometer, ASTM International, West Conshohocken, PA.
Chow, V. T. (1959). Open-Channel Hydraulics. New York, USA: McGraw-Hill.
Coello Granda, C. (2005) Análisis de métodos de estimación de la conductividad hidráulica saturada en suelos degradados. Tesis, Magister de Ciencias en Manejo y Conservación del Agua y del Suelo. Universidad de Cuenca.
Dafonte, D. J., Valcársel, A. M., Neira, X. X., & Paz, A. (1999). Análisis de los métodos de cálculo de la conductividad hidráulica saturada de campo medida con permeámetro Guelph. In Estudios de la Zona No Saturada del Suelo (Muñoz-Carpena, R.; Ritter, A.; Tascón, C.; editores). Libro, p. 5-10FETTER, C.W. 2001. Applied Hydrogeology, Fourt Edition. USA: Prentice Hall.
Fetter, C. W. (2001,1994). Applied Hydrogeology. 3rd ed. New Jersey, USA: Macmillan College Publishing Comp.
García-Sinovas, D., Regalado, C., Muñoz-Carpena, R., & Álvarez-Benedí, J. (2001). Comparación de los permeámetros de Guelph y Philip-Dunne para la estimación de la conductividad hidráulica saturada del suelo. En: Temas de Investigación en Zona no Saturada, J.J. López, M. Quemada (eds.), pp. 31-36. Pamplona.
Gerard-Marchant, P., Angulo-Jaramillo, R., Haverkamp, R., Vauclin, M., Groenevlet, P., & Elrick, D. E. (1997). Estimating the hydraulic conductivity of slowly permeable and swelling materials from single-ring experiments. Water Research, 33 (6), 1375-1382.
Green, W. H. & Ampt, G. (1911). Studies of Soil Physics, Part I – The Flow of Air and Water Through Soils. Journal of AgriculturalScience, 4, 1-24.
Gurovich, L. A. (1985). Fundamentos y diseño de sistemas de riego. Instituto Interamericano de cooperación para la agricultura. San José, Costa Rica.
Horton, R. E. (1939). Analysis of runoff-plat experiments with varying infiltration capacity. Transactions, American Geophysical Union, 20, 693-711.
Horton, R.E. (1940). An approach toward a physical interpretation of infiltration capacity. Soil Science Society of America Processes, 5, 399-417.
Kessler, J., & Oosterbaan, R. J. (1994). Determining Hydraulic Conductivity of Soils. Drainages Principles and Applications, v. 3. Publ. 16, International Institute for Land Reclamation and Improvement P. O. Box 45, Wageningen, The Netherlands, pp. 253-296.
Kostiakov, A. (1932). On the dynamics of the coefficient of water percolation in soils and necessity for studying it from a dynamic view for purposes of amelioration. International CommitteeSociety of SoilScience, 61(A), 17-21.
La Gaceta 243. (2010). Reglamento de Metodologías Hidrogeológicas para la evaluación del Recurso Hídrico. Imprenta Nacional de Costa Rica. N° 243-88 págs. San José, Costa Rica. p. 35.
Mendenhall, W. & Reinmuth, J. E. (1981). Estadística para administración y economía. México: Grupo Editorial Iberoamericana.
Nave, M. R., Pedrani, A., Vich, A., & Mariani, A. (1994). Ajuste del modelo de Horton mediante datos de infiltración obtenidos en el pie de monte mendocino. INIGEA. MULTEQUINA 3, 133-140.
Parr, J. F. & Bertrand, A. R. (1960). Water infiltration in soils. Advances in Agronomy, 12, 311-363.
Prieto, B., Támara, R., & Peroza, J. (2006). Comparación de dos métodos de campo para la determinación de la conductividad hidráulica saturada en suelos del Sinú (Córdoba, Colombia). Revista Temas Agrarios, Universidad de Córdoba, 76-103, 36-44.
Reynolds, W. D., & Elrick, D. E. (1986). A method for simultaneous in situ measurement in the vadose zone of field saturated hydraulic conductivity, sorptivity and the conductivity-presure head relationship. Ground Water Monitoring Review, 6 (1), 84-95.
Reynolds, W. D., Elrick, D. E., Youngs, E. G., Amoozegar, A., Booltink, H. W. G., & Bouna, J. (2002). Saturated and field-saturated wáter flow parameters. In: Methods of soil Analysis, Part 4-Physical Methods, Dane J.H. &Topp, (Eds.). Soil Science Society of America. Madison, USA. p 797-878.
Schosinsky, G. (2006). Cálculo de la recarga potencial de acuíferos mediante un balance hídrico de suelos. Revista Geológica de América Central, 34-35, 13-30.
Selker, J.S., Duan, J., & Parlange, J. (1999). Green and Ampt infiltration into soils of variable pore size with depth. Water Resources Research, 35: doi: 10.1029/1999WR900008. issn: 0043-1397
Steer, I. V. & Rodriguez, L. (2008). Diagnóstico de la infiltración y permeabilidad en los suelos de la zona de recarga del acuífero Morroa en el área Sincelejo, Corozal y Morroa. Tesis, Universidad de Sucre. Ecuador.
Talsma, T., & Hallam, P. M. (1980). Hydraulic conductivity measurement of Forest Catchments. Aust. J. Soil. Res., 18, 139-148.
Ven Te Chow, et al. (1994). Hidrología Aplicada. Primera Edición. Colombia: Editorial NOMOS S. A. McGRAW-HILL.
Wu, L., Swan, & Nieber, J. B. (1993). J. Soil-macropore and layer influences on saturated hydraulic conductivity measured with borehole permeameters. Soil Sci. Soc. Am. J., 57, 917-923.
Youngs, E. G., Leeds-Harrison, P. B., & Elrick, D. E. (1995). The hydraulic conductivity of low permeability wet soil used as landfill lining and capping material: analysis of pressure infiltrometer measurements. Soil Technology, 8,153-160.